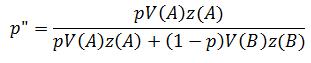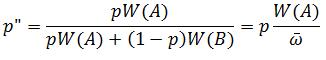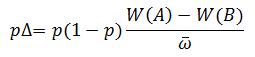Culture, its evolution and anything inbetween
Continuing my series on the Evolution of Colour terms, this post reviews evidence for environmental constraints on colour perception. For the full dissertation and for references, go here.
Continue reading “Evolution of Colour Terms: 2 Environmental Constraints”
Continuing my series on the Evolution of Colour terms, this post reviews the evidence for genetic constrains on colour perception. For the full dissertation and for references, go here.
Continue reading “Evolution of Colour Terms: 1 Genetic Constraints”
In a series of posts, I’ll review the current state of the field of the Evolution of Colour Categories. It has been argued that universals in colour naming across cultures can be traced back to constraints from many domains including genetic, perceptual and environmental. I’ll review these arguments and show that if our perception is affected by our language, then many conflicts can be resolved. Furthermore, it undermines the Universalist assumption that universal patterns in colour terms are evidence for innate constraints.
Part 1: Domains of Constraint
Part 2: Universal patterns are not evidence for innate constraints
Universal Patterns are not Evidence for Innate Constraints
For the full dissertation and for references, go here.
The way children learn language sets the adaptive landscape on which languages evolve. This is acknowledged by many, but there are few connections between models of language acquisition and models of language Evolution (some exceptions include Yang (2002), Yu & Smith (2007) and Chater & Christiansen (2009)).
However, the chasm between the two fields may be getting smaller, as theories are defined as models which are both more interpretable to the more technically-minded Language Evolutionists and extendible into populations and generations.
Also, strangely, models of word learning have been getting simpler over time. This may reflect a move from attributing language acquisition to specific mechanisms towards a more general cognitive explanation. I review some older models here, and a recent publication by Fazly et al.
Continue reading “Language Evolution and Language Acquisition”
How is it, then, that we can talk about talking? If you are willing to assume the existence of basic perceptual and cognitive capacities, a relatively simple answer follows immediately. The sounds of talk are, after all, sounds like any other sounds. We can perceive them in the same way we perceive the sound of a waterfall or a bird’s song, a thunderclap or the rustling of leaves in the wind, a cricket’s chirp or the breaking of waves on a beach. All are things we can hear, easily and naturally, and so it is with the sound of the human voice.
Roman Jakobson famously theorized that language has six functions: referential, emotive, poetic, conative, phatic, and the metalingual function. That’s the function we’re interested in, our capacity to speak about speech. Jakobson talked of the metalingual function as an orientation toward the language code, which seems just a bit grand. For I’m led to believe that many languages lack terms for explicitly talking about the ‘code.’ Thus, in The Singer of Tales (Atheneum 1973, orig. Harvard 1960), Albert Lord attests (p. 25):
Man without writing thinks in terms of sound groups and not in words, and the two do not necessarily coincide. When asked what a word is, he will reply that he does not know, or he will give a sound group which may vary in length from what we call a word to an entire line of poetry, or even an entire song. [Remember, Lord is writing about oral narrative.] The word for “word” means an “utterance.” When the singer is pressed then to way what a line is, he, whose chief claim to fame is that he traffics in lines of poetry, will be entirely baffled by the question; or he will say that since he has been dictating and has seen his utterances being written down, he has discovered what a line is, although he did not know it as such before, because he had never gone to school.
While I’m willing to entertain doubts about the full generality of this statement – “man without writing” – I assume the it is an accurate report about the Yugoslavian peasants among whom Milman Parry and Albert Lord conducted their fieldwork and that it also applies to other preliterate peoples, though not necessarily to all.
Given those caveats, the paragraph is worth re-reading. Before doing so, recall how casually we have come to see language as a window on the workings of the mind in the Chomskyian and post-Chomskyian eras. If that is the case, then what can one see through a window that lacks even a word for words, that fails to distinguish between words and utterances? And what of the poets who don’t know what a line is? The lack of such knowledge does not stand in the way of the poeticizing, no more than the lack of knowledge of generative grammar precludes the ability to talk intelligently on a vast range of subjects.
So in my previous post on mathematical modelling I looked at viability selection and how it can be expressed using relatively simple mathematics. What I didn’t mention was fertility. My reasoning largely being because the post was already getting unwieldy large for a blog, and, from now on, I’m going to limit the length on these math-based posts. I personally find I get more out of small, bite-sized chunks of information that are easily digestible, than overloading myself by trying understand too many concepts all at once. With that said, I’ll now look at what happens when the two zygote types, V(A) and V(B), differ in their fertility.
A good place to start is by defining the average number of zygotes produced by each type as z(A) and z(B). We can then plug these into a modified version of the recursion equation I used in the earlier post:
So now we can consider both fertility and viability selection. Furthermore, this can be combined to give us W(A) = V(A)z(A) and W(B) = V(B)z(B):
Remember, 
, is simply the the average the fitness in the population, which can be used in the following difference equation:
That’s it for now. The next post will look at the long-term consequences of these processes.
Reference: McElreath & Boyd (2007). Mathematical Models of Social Evolution: A guide for the perplexed. University of Chicago Press. Amazon link.
If you go to this page at Linguistic Inquiry (house organ of the Chomsky school), you’ll find this blurb:
Episode 3: Samuel Jay Keyser, Editor-in-Chief of Linguistic Inquiry, has shared a campus with Noam Chomsky for some 40-odd years via MIT’s Department of Linguistics and Philosophy. The two colleagues recently sat down in Mr. Chomsky’s office to discuss ideas on language evolution and the human capacity for understanding the complexities of the universe. The unedited conversation was recorded on September 11, 2009.
I’ve neither listened to the podcast nor read the transcript—both linked available here. But who knows, maybe you will. FWIW, I was strongly influenced by Chomsky in my undergraduate years, but the lack of a semantic theory was troublesome. Yes, there was co-called generative semantics, but that didn’t look like semantics to me, it looked like syntax.
Then I found Syd Lamb’s stuff on stratificational grammar & that looked VERY interesting. Why? For one thing, the diagrams were intriguing. For another, Lamb used the same formal constructs for phonology, morphology, syntax and (what little) semantics (he had). That elegance appealed to me. Still does, & I’ve figured out how to package a very robust semantics into Lamb’s diagrammatic notation. But that’s another story.
The limitations of geological periods, imposed by physical science, cannot, of course, disprove the hypothesis of transmutation of species; but it does seem sufficient to disprove the doctrine that transmutation has taken place through ‘descent with modification by natural selection’. — Lord Kelvin (Of Geological Dynamics, 1869).
It might seem odd that I start a post about evolution with a quote claiming natural selection is inadequate to account for the transmutation of species. It is, though, highly relevant to what I’m going to discuss in the post, and strikes at the heart of why it’s fundamental for us to understand the theory of evolution by natural selection. See, in 1869, Lord Kelvin’s position was fairly reasonable, and, as you’d expect for a man of such high scientific standing, the available evidence in physics did seem to conflict with Darwin’s theory. The Sun was one particularly salient point of contention: to get the diversity of species we see on Earth, evolution needs a long time to work (on the order of hundreds of millions, if not billions of years), yet according to 19th-century physics the Sun could only have been burning for 40-million years.
Continue reading “A history of evolution pt.1: Ancient Greece to Lamarck”
I think the best place to start would be to state the following: Do not fear math. I spent far too long dodging equations and, when that wasn’t possible, freezing in a state of absolute confusion when faced with something like:
By the end of this post, you’ll hopefully be able to understand the above is not just a bunch of jibberish. Now before we get into the nitty gritty of the subject, I think a clarification of my assumptions is in order:
Continue reading “Mathematical Modelling 101: Introduction & Viability Selection”
