Mathematical Modelling 101: Introduction & Viability Selection

I think the best place to start would be to state the following: Do not fear math. I spent far too long dodging equations and, when that wasn’t possible, freezing in a state of absolute confusion when faced with something like:

By the end of this post, you’ll hopefully be able to understand the above is not just a bunch of jibberish. Now before we get into the nitty gritty of the subject, I think a clarification of my assumptions is in order:

1. That you’ll have a basic understanding of evolutionary biology. If not, then may I suggest Evolution as a very good, and highly comprehensive, introductory text. Failing that, you can always pop over to the wikipedia page.
2. Although these posts will refer to evolutionary biology, my background is in linguistics and socio-cultural evolution — and as such, I will tend to default to the position of explaining these latter areas.
3. It might sound insulting, but you’ll also need a basic understanding of math. You’ll be surprised by the number of people who, despite being very bright, lack even an elementary grasp of the fundamentals. A good place to start is with Kahn Academy’s wonderful online resource: http://www.khanacademy.org/.
4. Having said that, I’m not really expecting anything beyond algebra level math, and I’ll do my best to try and clarify any confusions in the comments section. Also, I’m hardly a math guru, so I welcome anyone with a solid background in math to provide any hints, tips or suggestions, and, in the event I’m plain wrong, point out any mistakes.

Viability Selection

One of the best places to start is a form of natural selection which population geneticists refer to as viability selection: the probability of an individual surviving until adulthood, where it can then reproduce. To get an idea of where viability selection is as a component of natural selection I’ve taken the following diagram from wikipedia:

For the basics of any evolutionary model, the minimum requirements are:

1. The number of individuals and how they are socially organised in the Population.
2. A set of Heritable Variants.
3. The events influencing the survival and spread of heritable variants across a Life Cycle

The goal of our model, then, is to mathematically describe how events in the life cycle change the distribution of heritable variants in the population over one time period. What we want to be looking at is selection for survival. Models are generally abstractions, or simplifications, of events taking place in the natural world. A good way to narrow your focus is to make a list of assumptions. In this case, there are a few assumptions we need to highlight:

• There is a population of n individuals, with n being large enough to avoid sampling variation;
• Individuals within this population are haploid — so no sex or recombination (sorry, guys!).
• There are only two genotypes: Genotype A and Genotype B;
• Everyone is born at the same time, and every reproduces at the same time — that is, their life cycle is in lock step;

Now, we are going to have n zygotes exist at a particular time t. Under this scenario, there is no difference in the type of zygotes who are able to survive into adults, with A types being no more likely to survive than B types. Those that survive then go onto to reproduce, creating a population of zygotes at a time t + 1. In moving through time, a useful ability to have is keeping track of the frequencies of different genotypes within a population. Normally, these frequencies are between 1 and 0, which simply tells us what fraction of the population is of a certain type. This is an example of what we call state variables: A set of variables describing the state of a dynamical system, with the quantities in our case being enough to determine its future behaviour. Applied to our two types, A and B, then the frequency of A, p_A, tells us the portion of the population of type A. In population genetic models, the tendency is for the number of state variables to be one less than the number of alternative alleles. As we only have two types, it is relatively simple to work out the proportion that is type B: you simply subtract the total proportion by the frequency of A (1 — p_A).

Given the simplicity of this model, only one evolutionary force is taking place: individuals with some genotypes are more likely to survive than others. To look at the consequences of survival across a period of time, we need to look at the genotypes at time t and at time t + 1. So, if p is the frequency of the A genotype in the population at time t, then we can express it as the following:

Here, n is the number of individuals within the population. So the number of A zygotes is equal to np. As such, the number of B zygotes is n(1 — p). With a single number, p, we are now able to keep track of the differential evolution of types A and B. The value of p is flexible in the sense that in the next stage of the life cycle p might change. To provide a representation of our state variable in its next stage we use p’ (p prime).

But what happens when these zygotes mature?

Well, some will survive into adulthood, so we need to look at probabilities of both A type and B type zygotes: V(A) and V(B). For example, when V(A) = 0.5, we know that the probability of an A type zygote will survive into adulthood is 50%. Conversely, we also know that V(B) = 0.5. Next, we need to work out the number of adults with genotype A, which is simply:

number of A adults = number of individuals in a population * the frequency of the A genotype in the population at time t * V(A).

number of A adults = npV(A).

The number of B adults is then n(1 — p)V(B). Next, I want to find the frequency of genotype A among adults at p’ :

The left over adults will now mate and subsequently reproduce. As they are reproducing asexually, the adults produce z zygotes, regardless of genotype. Now we want to find the frequency of genotype A at t + 1:

As you can see: reproduction does not change the frequencies of A and B genotypes. So you can write the following recursive expression for the frequency of genotype A after one generation:

As this expression is a recursion, we can modify it to calculate the frequency of genotype A in in subsequent generations by substituting the previous generation into the recursion. Whilst repeating the equation for each generation is fine, there is, however, another method McElreath & Boyd refer to: a difference equation. To derive a difference equation for the above recursion, then you simply do the following (taken from McElreath & Boyd, 2007, pg. 15):

For your own reference, , is the change in frequency of A from time t to time t + 1, and if we use the expression, then we get the following:

So, we’re back at the start, and you should now have some understanding of what the above equation means in regards to how natural selection changes genotype frequencies. To help clarify, the equation can be broken up into two parts:

1. p(1 — p) is simply the variance in genotypes in the population: when there is no variation (p = 1 or 0), natural selection will be unable to change genotype frequencies. You see, natural selection needs variation with which to work, so when variance is maximized (p = 0.5) natural selection is at its strongest.
2. The second part of the equation, 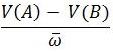, is the proportional increase or decrease of genotype A to genotype B. As long as there is some variation in genotypes, and assuming one genotype is more fit than the other, then the frequency of one of the genotypes will increase each generation. Conversely, the frequency of the other genotype will decrease at each generation.

Reference: McElreath & Boyd (2007). Mathematical Models of Social Evolution: A guide for the perplexed. University of Chicago Press. Amazon link.

N.B. All examples and equations are adapted from Chapter 1 of the aforementioned book as it’s one of the best introductory texts I’ve read. I strongly suggest that, if you’re interested, you’ll click on the above Amazon link and buy the book.