Poets are the unacknowledged legislators of the world.
– Percy Bysshe Shelley
… it is precisely because we are talking about ordinary language that we need to adopt a notation as different from ordinary language as possible, to keep us from getting lost in confusion between the object of description and the means of description.
¬–Sydney Lamb
Worlds within worlds – that’s how Tim Perper, my friend and colleague, described biology. At the smallest scale we have individual molecules, with DNA being of prime importance. At the largest scale we have the earth as a whole, with all living beings interacting in a single ecosystem over billions of years. In between we have cells, tissues, and organs of various sizes, autonomous organisms, populations of organisms on various scales from the invisible to continent-spanning, and interactions among populations of organisms on various scales.
Literature too is like that, from single figures and tropes, even single words (think of Joyce’s portmanteaus) through complete works of various sizes, from haiku to oral epics, from short stories through multi-volume novels, onto whole bodies of literature circulating locally, regionally, across continents and between them, from weeks and years to centuries and millennia. Somehow we as humanists and literary critics must comprehend it all. Breathtaking, no?
In this essay I sketch a potential computational historicism operating at multiple scales, both in time and textual extent. In the first part I consider network models on three scale: 1) topic models at the macroscale, 2) Moretti’s plot networks at the mesoscale, and 3) cognitive networks, taken from computational linguistics, at the microscale. I give examples of each and conclude by sketching relationships among them. I open the second part by presenting an account of abstraction given by David Hays in the early 1970s; in this model abstract concepts are defined over stories. I then move on to Hauser and Le-Khac on 19th Century novels, Stephen Greenblatt on self and person, and consider several texts, Amleth, Hamlet, The Winter’s Tale, Wuthering Heights, and Heart of Darkness.
Graphs and Networks
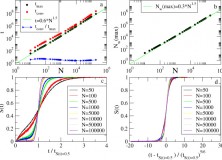
To the mathematician the image below depicts a topological object called a graph. Civilians tend to call such objects networks. The nodes or vertices, as they are called, are connected by arcs or edges.
Such graphs can be used to represent many different kinds of phenomena, a road map is an obvious example, a kinship tree is another, sentence structure is a third example. The point is that such graphs are signs of phenomena, notations. They are not the phenomena itself. Continue reading “Toward a Computational Historicism. Part 1: Discourse and Conceptual Topology”