So in my previous post on mathematical modelling I looked at viability selection and how it can be expressed using relatively simple mathematics. What I didn’t mention was fertility. My reasoning largely being because the post was already getting unwieldy large for a blog, and, from now on, I’m going to limit the length on these math-based posts. I personally find I get more out of small, bite-sized chunks of information that are easily digestible, than overloading myself by trying understand too many concepts all at once. With that said, I’ll now look at what happens when the two zygote types, V(A) and V(B), differ in their fertility.
A good place to start is by defining the average number of zygotes produced by each type as z(A) and z(B). We can then plug these into a modified version of the recursion equation I used in the earlier post:
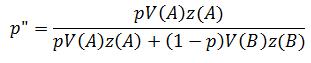So now we can consider both fertility and viability selection. Furthermore, this can be combined to give us W(A) = V(A)z(A) and W(B) = V(B)z(B):
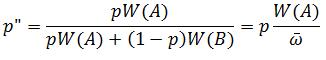Remember, 
, is simply the the average the fitness in the population, which can be used in the following difference equation:
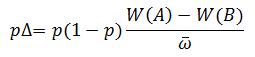That’s it for now. The next post will look at the long-term consequences of these processes.
Reference: McElreath & Boyd (2007). Mathematical Models of Social Evolution: A guide for the perplexed. University of Chicago Press. Amazon link.