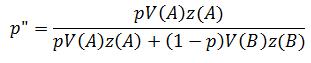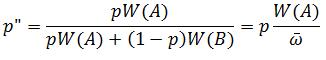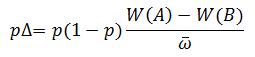mathematical modelling – Replicated Typo

Mathematical Modelling 101 – The Price Equation

So in this post I’m going to assume you know absolutely nothing about anything. If you know something about something this probably isn’t what you’re looking for. If you’re looking for something which will go into depth on how the price equation is derived this probably isn’t what you’re looking for either. If you simply want to know what the price equation does and how to use it at face value then welcome! You’ve found the right place.

The price equation is used to calculate how the average value of any variant can change within a population from generation to generation.

Here I will cover everything you need to know to understand the equation and slot in the right values:

Continue reading “Mathematical Modelling 101 – The Price Equation”

Animal Signalling Theory 101 – The Handicap Principle

One of the most important concepts in animal signalling theory, proposed by Amotz Zahavi in a seminal 1975 paper and in later works (Zahavi 1977; Zahavi & Zahavi 1997), is the handicap principle. A general definition is that females have evolved mating preferences for males who display exaggerated ornaments or behaviours that are costly to maintain and develop, and that this cost ensures an ‘honest’ signal of male genetic quality.

As a student I found it quite difficult to identify a working definition for this important type of signal mainly due to the apparent ‘coining fest’ that has taken place over the years since Zahavi outlined his original idea in 1975. For this reason, I have decided to provide a brief outline of the terminological and conceptual differences that exist in relation to the handicap principle in an attempt to help anyone who might be struggling to navigate the literature.

As Zahavi did not define the handicap principle mathematically, a number of interpretations can be found in the key literature due to scholars disagreeing as to the true nature of his original idea. Until John Maynard Smith and Harper simplified and clarified things wonderfully in their 2003 publication Animal Signals, to my knowledge at least four different interpretations of the handicap were being used and explored empirically and through mathematical modelling, each with distinct differences that aren’t all that obvious to grasp without delving into the maths.

Continue reading “Animal Signalling Theory 101 – The Handicap Principle”

Selection on Fertility and Viability

So in my previous post on mathematical modelling I looked at viability selection and how it can be expressed using relatively simple mathematics. What I didn’t mention was fertility. My reasoning largely being because the post was already getting unwieldy large for a blog, and, from now on, I’m going to limit the length on these math-based posts. I personally find I get more out of small, bite-sized chunks of information that are easily digestible, than overloading myself by trying understand too many concepts all at once. With that said, I’ll now look at what happens when the two zygote types, V(A) and V(B), differ in their fertility.

A good place to start is by defining the average number of zygotes produced by each type as z(A) and z(B). We can then plug these into a modified version of the recursion equation I used in the earlier post:

So now we can consider both fertility and viability selection. Furthermore, this can be combined to give us W(A) = V(A)z(A) and W(B) = V(B)z(B):

Remember, , is simply the the average the fitness in the population, which can be used in the following difference equation:

That’s it for now. The next post will look at the long-term consequences of these processes.

Reference: McElreath & Boyd (2007). Mathematical Models of Social Evolution: A guide for the perplexed. University of Chicago Press. Amazon link.