On the weekend I did an analysis about a recent paper by Caleb Everett linking altitude to the presence of ejective sounds in a langauge. In this post I look at the possible effects of contact and population size. I find that controlling for population size removes the significance of the link between ejectives and elevation.
In a comment on the post, Chris Lucas suggested that languages at higher altitudes might be more isolated, and so less subject to contact-induced change:
“contact tends to make languages lose ejectives, if they ever had them. The reasoning here would be that a language’s having (contrastive) ejectives implies that it has a large consonant inventory, which implies that it does not have a history of significant numbers of people having learnt it as a second language, since this tends to lead to the elimination of typologically rare features.”
We can test this in the following way: We can get a rough proxy for langauge contact for a community by counting the number of languages within 150km (range between 0 and 44). If we run a phylogenetic genralised least squares test, predicting the presence of ejectives by elevation and number of surrounding languages, we get the following result (estimated lambda = 0.8169142 , df= 491, 489):
| Coefficient | Std.Error | t-value | p-value | |
| Elevation | 0.00004514 | 0.00001655 | 2.728177 | 0.0066 ** |
| No. surrounding langs | -0.00312549 | 0.00147532 | -2.118507 | 0.0346 * |
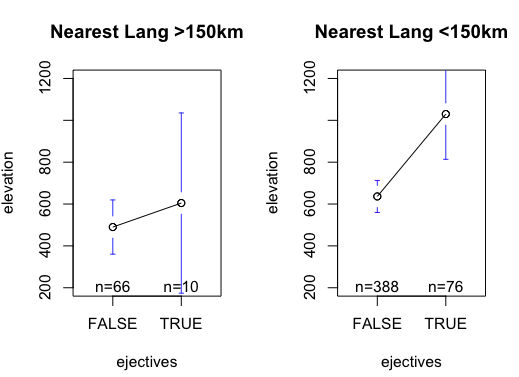
While elevation is still significant, the number of surrounding languages is also a significant predictor (the effect size is also greater). The greater the number of surrounding languages, the smaller the chance of a langauge having a ejectives. This fits with the idea that contact induced change removes ejectives, rather than air pressure being the only cause. In the graph below, I’ve plotted the mean elevation for languages with and without ejectives, comparing languages with a neighbour within 150km and languages without a neighbour in 150km. The effect is stronger in the group with neighbouring languages (right), which would fit with languages loosing ejectives due to contact.
However, it’s not quite so simple, since we have to take into account the relative relatedness of languages. If we count the number of distinct language families within 150km, then the significance goes away:
| Coefficient | Std.Error | t-value | p-value | |
| Elevation | 0.00003893 | 0.00001645 | 2.366329 | 0.0184 * |
| No. surrounding families | 0.00348498 | 0.0074656 | 0.466806 | 0.6408 |
What about another proxy for contact, like population size (as used by Lupyan & Dale, 2010)? I took speaker populations from the Ethnologue and ran another PGLS:
| Value | Std.Error | t-value | p-value | |
| Elevation | 0.00001786 | 0.00001962 | 0.910439 | 0.3632 |
| Log population | -0.0110823 | 0.00817542 | -1.355564 | 0.1761 |
Now we see that neither variable is significant, though larger populations tend not to have ejectives. That is, by controlling for linguistic descent and population size, the correlation between elevation and ejectives goes away.
In fact, a simple logit regression predicting elevation by elevation and log population results in the following:
| Estimate | Std.error | z-value | Pr(>|z|) | ||
| (Intercept) | -0.6579524 | 0.3874394 | -1.698 | 0.089469 . | |
| Elevation | 0.0003757 | 0.0001665 | 2.257 | 0.024014 * | |
| Log population | -0.327502 | 0.0920464 | -3.558 | 0.000374 ** |
We can see that, even if we don’t control for phylogeny, population size is a better predictor of ejectives than elevation (although Everett uses several measures of altitude).
I also wondered if the distance to the nearest language could be a proxy for contact. Let’s put all the variables into one regression.
| Value | Std.Error | t-value | p-value | |
| Elevation | 0.0000257 | 0.00001988 | 1.290864 | 0.1976 |
| No. surrounding languages | -0.0069331 | 0.00278402 | -2.490329 | 0.0132 * |
| Minimum distance to nearest language |
-0.0001173 | 0.00011222 | -1.04528 | 0.2966 |
| Log population | -0.011234 | 0.0081391 | -1.380251 | 0.1684 |
Here we see that the number of surrounding languages is still a significant predictor of the presence of ejectives (although using the number of surrounding families doesn’t work), but elevation is not.
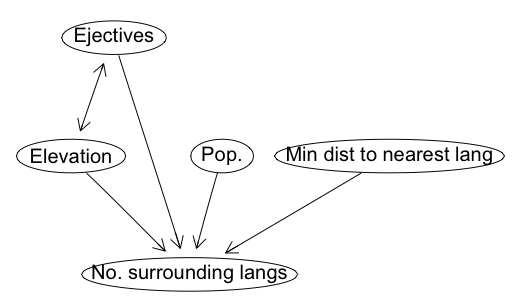
We can build the most likely causal graph (see my post here) for the data above. This ignores the phylogenetic relatedness of langauges, but allows us to explore more complex relationships between all the variables. Below, we see that elevation and ejectives are still linked, as Everett would predict.
The stats I’ve presented here are just rough explorations of the data, not proof or disproof of any theory. Here are some issues that are still unresolved:
- What about the distance from high-elevation areas, as used in Everett’s paper?
- Are the proxies above reasonable?
- What is the likelihood of keeping ejectives versus losing them during contact?
- In the analyses above, I’m not controlling for geographical relatedness, this could be done by selecting independent samples or Mantel tests.
- There are links between phoneme inventory size, the geographic area a langauge covers, morphology and demography (see James’ posts here and here). What is the best way to approach the complex relationships between these features?
Of course, laboratory experiments or careful idographic work could address these issues better than more statistics.

When you say “the effect size is also greater” and later “is a better predictor” (elevation being the smaller/worse predictor), what do you mean exactly?
Thanks a lot for following up on my comment – much appreciated. I like what you’ve done here. I will say though that I much prefer population size to number of languages spoken as a proxy for the relevant type of language contact. This is for two reasons. 1) I believe that there are certain areas of the world (usually mountainous areas!) where there are fairly large numbers of languages spoken relatively close to one another as the crow flies, but which do not have a significant history of contact because local geography makes this difficult. I believe highland PNG is an example of this, but others who know better can perhaps correct me here. 2) The second point bears on the third question in your post: What is the likelihood of keeping ejectives versus losing them during contact? The answer to this is that it depends on the type of contact. If the type of contact involves long-term stable bilingualism, then the likelihood of a language keeping ejectives and indeed passing them on to a contact language is high. Asya Pereltsvaig gives a number of examples of contact-induced spread of ejectives in the latest Geocurrents post. As pointed out by Trudgill in his 2011 book ‘Sociolinguistic typology’, long term stable bilingualism tends to lead to phonological and morphological complexification in the languages in contact. On the other hand, when contact involves large numbers of adults learning the language in question as a second language, this tends to result in phonological and morphological simplification. I would have thought that a language having a relatively large number of speakers is a reasonable indication that it has a history of this sort of contact. Or better: a language having a small number of speakers is a reasonable indication that it doesn’t have this kind of history.
Good points!
Hi,
Sorry, I wasn’t clear. In the first case, I meant that the coefficeint for the number of surrounding families is greater than the coefficient for elevation. Population size is a better predictor in the sense that it has a lower p-value than elevation, so is better at predicting the presence of ejectives.
great work!
Nice work. So there’s still some link (though weakened) between elevation, even with the absolute elevation data? What we really need though is a reanalysis of the distance data, since the geographic clustering is claimed to be the crucial stuff. I’m surprised you can say you “removed a link” without looking at those data. Doesn’t this also point to a different sort of indirect geographic effect, given the role of geography in impacting population sizes and distribution points? Oh and I guess what we really, really need is lab work as you suggest. Again, though, nice work.
The logit regression model above that shows a weak effect of elevation doesn’t take into account the historical relatedness of languages (the other test above do take phylogeny into account). However, you’re right – Everett’s main variable is distance from high altitude areas. What I hope I’ve shown is that he should also control for population size.