It is one thing to use computers to crunch data. It’s something else to use computers to simulate a phenomenon. Simulation is common in many disciplines, including physics, sociology, biology, engineering, and computer graphics (CGI special effects generally involve simulation of the underlying physical phenomena). Could we simulate large-scale literary processes?
In principal, of course. Why not? In practice, not yet. To be sure, I’ve seen the possibility mentioned here and there, and I’ve seen an example or two. But it’s not something many are thinking about, much less doing.
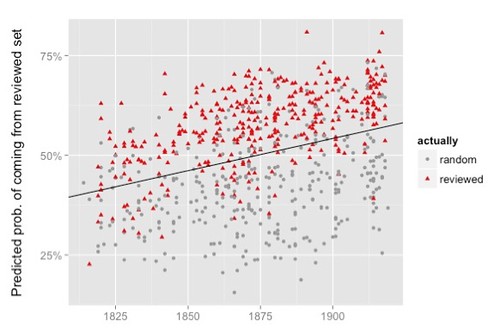
Nonetheless, as I was thinking about How Quickly Do Literary Standards Change? (Underwood and Sellers 2015) I found myself thinking about simulation. The object of such a simulation would be to demonstrate the principle result of that work, as illustrated in this figure:
Each dot, regardless of color or shape, represents the position of a volume of poetry in a one-dimensional abstraction over 3200 dimensional space – though that’s not how Underwood and Sellers explain it (for further remarks see “Drifting in Space” in my post, Underwood and Sellers 2015: Cosmic Background Radiation, an Aesthetic Realm, and the Direction of 19thC Poetic Diction). The trend line indicates that poetry is shifting in that space along a uniform direction over the course of the 19th century. Thus there seems to be a large-scale direction to that literary system. Could we create a simulation that achieves that result through ‘local’ means, without building a telos into the system?
The only way to find out would be to construct such a system. I’m not in a position to do that, but I can offer some remarks about how we might go about doing it.
* * * * *
I note that this post began as something I figured I could knock out in two or three afternoons. We’ve got a bunch of texts, a bunch of people, and the people choose to read texts, cycle after cycle after cycle. How complicated could it be to make a sketch of that? Pretty complicated.
What follows is no more than a sketch. There’s a bunch of places where I could say more and more places where things need to be said, but I don’t know how to say them. Still, if I can get this far in the course of a week or so, others can certainly take it further. It’s by no means a proof of concept, but it’s enough to convince me that at some time in the future we will be running simulations of large scale literary processes.
I don’t know whether or not I would create such a simulation given a budget and appropriate collaborators. But I’m inclined to think that, if not now, then within the next ten years we’re going to have to attempt something like this, if for no other reason than to see whether or not it can tell us anything at all. The fact is, at some point, simulation is the only way we’re going to get a feel for the dynamics of literary process.
* * * * *
It’s a long way through this post, almost 5000 words. I begin with a quick look at an overall approach to simulating a literary system. Then I add some details, starting with stand-ins (simulations of) texts and people. Next we have processes involving those objects. That’s the basic simulation, but it’s not the end of my post. I have some discussion of things we might do with this system followed with suggestions about extending it. I conclude with a short discussion of the E-word.
The literary system, a first sketch
The first thing we need to do is figure out what to include in the simulation. Underwood and Sellers have stated the basic requirements as “the system of interaction between writers, readers, and reviewers” (p. 21) and, of course, text. While reviews provide evaluations and we might expect those to influence readers, Underwood and Sellers didn’t take that into account. They simply noted whether or not a volume was reviewed. Let us therefore assume that the major effect of reviews is simply to make texts more visible in the population. The more visible a text is, the more likely people will read it. Let us further assume that the effect of being read is to increase the likelihood that more texts like it will be produced in the future.
How could we model this? AS I began thinking about this I realized that the basic problem is to come up with some simulation of literary process. The effect of elite reviews is one of the things we want to look at in the simulation, but it’s not necessarily the only thing we could investigate.
Operationalizing the sketch
We’re going to have two kinds of objects in our simulated universe: texts and people. Both texts and people need to have identities (names or some sort) and they must features of some sort. The features of text objects are stand-ins for contents of real texts. The features of people objects are stand-ins for reading preferences. These two sets of features must be commensurable so that we can compute the ‘match’ between a person and a text. The closer the match, the more likely the person will read the text. The effect of reviews must also be stated in the same terms.
We are going to need a number of processes through which these two populations interact. For the purposes of simulation let us assume that the literary system operates in discrete cycles. If you wish, you can think of each cycle as corresponding to a year, or a month, or a week, whatever. It really doesn’t matter since, as you will see shortly, my proposals for representing texts and people are so highly schematic that such things as years and days are but labels of convenience.
The cycle is the largest scale process our simulation has. Or rather, it’s the succession of cycle’s that’s the largest scale process. We aren’t going to provide the simulation with any goal that it’s going to steer toward in the succession of cycles. That’s teleology and it’s cheating. Any large-scale structure exhibited by the system will be the ‘emergent’ result of the succession of one cycle by another.
I figure that we need roughly three processes within each cycle:
• We need a process that gets readers in touch with texts; call that publishing.
• Computing a match between a text and a person is another processes in the model; call it reading.
• And then we need a reviewing process that interacts with the reading process.
To run the simulation we need to initialize the process by creating initial populations of people objects and of text objects. We must also provide a set of ‘values’ for the review process. When the first cycle is complete we need some procedure for generating the next (and successive) cycles until we’ve run however many cycles we want to run.
How many texts and how many people do we create? I don’t know, but in the real world the number of people is generally considerably larger than the number of texts and the number of texts any one person reads is considerably smaller than the number available. How would things work if we had 100,000 people, 100 texts per cycle, and limited each person to reading 10 texts in a given cycle? The only way to find out would be to build a simulation and find out. I’d be inclined to make the number of people as large as is computationally feasible and to scale the other numbers accordingly.
Furthermore, for the purposes of discussion, I am going to make one very unrealistic assumption: the population of readers will remain unchanged throughout a given run of the simulation. It will remain unchanged in two senses: 1) no individuals will be dropped from the population nor will any new individuals be introduced into the population, and 2) an individual’s preferences will not change over the course of the run. Later on we might want to drop one or both of these conditions, something I will discuss briefly near the end.
Thus we will be simulating changes in the population of texts as people read through that population.
Characterizing texts
Let each text consist of a name (some unique identifier), its content, and a tally. The name is just that, a name; it’s device for keeping track of the text. The tally indicates how many times, if any, a text has been read. And that content is what is read.
In the case of real texts the content consists of words, phrases, sentences, paragraphs and so forth. And they instantiate things like genre and the associated conventions of each genre (plot, characters, and so forth), language and style, length (e.g. not everyone is up to reading a Victorian triple-decker) and whatever else, all the sorts of things literary critics study (and many that they don’t). But we’re not dealing with real texts. We’ve got a completely artificial situation. Furthermore I note that we’re running this simulation to get insight into patterns we observe through the various analytical and descriptive procedures of digital criticism (aka known as ‘distant’ reading). Those procedures work from highly abstracted versions of texts, abstracting them into so-called bags of words.
It’s not merely that our simulation isn’t going to capture the full richness of reality in all its abundance, but that we don’t even have access to that full richness. Digital criticism grants us access we’ve never had before. The object of simulation is to gain insight into the mechanisms revealed through those investigations.
For the purposes of discussion let us characterize each text by ten variables (aka features, traits), A, B, C…J, and that each variable can have one of ten numerical values, 0…9. That means that each text would be characterized by a list, or vector, of ten numerals. So, one text would have these characteristics, 9710452712; another would have these, 3055128563; another would have these, 4449426653; and so forth. This gives us 10^10 possible texts in our universe, which is ten billion (10,000,000,000) possible texts.
The number of (completely artificial) traits doesn’t have to be ten, of course. It could be five or 17, or 128. I have absolutely no feel for this and have no investment in any particular number of traits. My decision to use integer values for traits is somewhat different. We might be better off letting each trait be a real number between 0 and 1. But I don’t want to get bogged down in that discussion, which I can’t take very far in any event.
If we characterize texts in this way we could represent each text as a point in ten-dimensional space and calculate the distances between texts in the space (we may not want to be limited to integer values at this point). Those distances would be a measure of resemblance between texts.
As an exercise for the reader, consider basing simulated texts on real texts. In their investigation, Underwood and Sellers treated real texts simply as so-called bags of words, a list of words in each text along with the frequency of use. Why not use bags of words from real texts in the simulation?
Characterizing people and their reading preferences
In the case of real people, we’re talking about whatever it is that determines preferences for texts, personality, age, education, gender, whatever. This strikes me as, at best, a rather vague set of things, and one rather difficult to simulate in any remotely realistic way. But we’re not going to have our simulated people read real texts.
They’re going to read simulated texts, so it makes sense to characterize our people in the same terms we’ve used to characterize texts. Thus, if we characterize texts as a 10-item vector, then we can also characterize each reader’s preferences in terms those vectors. The simplest thing might be to assign each person one such vector that, in effect, characterizes that person’s ‘ideal’ text. It would then be relatively straightforward to calculate the distance between any text and any person (that is, the person’s idea text).
If you wanted to get fancier you might characterize each person by two or more such vectors, indicating that the person has multiple textual preferences–which, of course, many of us do. You might even designate a person by a certain volume such that any point within that volume is of the same value.
When we run a simulation we’re going to have to create a population of people. We can choose names for them however we will. The tricky business is giving them text preferences. The simplest thing might be to draw preferences randomly from the 10D space. Whether or not that’s the best thing, that’s another matter.
Creating and updating the text population
We need a text creation function (TCF) that creates a set of ‘published’ texts at the beginning of each cycle (year) of the model. To begin each simulation run we need to initialize this set by populating it with a bunch of texts. There are various ways we could do this. For example, we could create texts so that they are uniformly distributed throughout the 10-dimensional text space. Or we could draw the texts at random from in the space. This is rather different, as a random distribution of texts is likely to have local regions of high and low density that might be amplified in subsequent cycles. By definition such irregularities would not exist in a uniform distribution.
In the real world, of course, texts remain available in years subsequent to their original publication and popular texts will go through multiple printings and editions. Unpopular texts will still exist, but few will know about them.
Let us therefore assume that the text population for any cycle after the first will consist of a mixture of texts from previous cycles and new texts. Whether or not a text was carried over from previous cycles depends on whether or not it was read – something we’re tracking with each text’s tally. Let us also assume that the new texts in any given cycle will be a mixture of 1) texts biased in favor of texts like those that have previously been read and 2) texts created without any bias whatsoever.
On the first condition, if a text was read or, especially, read often, during cycle N, then the TCF will be more likely to create a new text exactly like it or closely resembling it (that is, near to it text space) in cycle N+1. In this case the new text can be said to be a descendent of that earlier text. This first condition guarantees that reader preference matters in the production of texts while the second condition allows for the creation of novelty. Such novelty may in fact capture aspects of reader preference that had gone unmet before.
Reading texts
I note that, whatever a person’s preferences may be, they can only read texts that 1) exist, and 2) they know about. For the purposes of this simulation let us assume that a person reads any text they know about that is sufficiently close to their preference space. If there are no known texts close enough to their preference space, they won’t read any texts at all.
What I propose is that, for each person, ranking all texts in the current population according to how closely they match that individual’s preference. Call it a preference ranking. But a person isn’t going to read the entire list. They’re only going to read the top N (10, 20, 57, whatever) items in the ranking and then stop. So:
1. Calculate the similarity between a person’s preference(s) and the list of texts published in the current cycle.
2. Enter them onto the person’s reading list starting with the most preferred.
3. Stop when the appropriate number of texts has been added to the list.
4. For each text on a person’s list, add one (1) to that text’s tally.
The value of a text’s tally will determine whether or not it is itself carried over into the next cycle or, if not that, whether or not it will have a ‘descendent’ in the next cycle.
The effect of reviews
Now that we’ve built all this basic machinery for simulating literary process, how can we use it to model the effect of reviews, that is, the effect of elite preference? That requires two things: 1) a way of characterizing those preferences, and 2) a way of having those preferences influence the operation of the system.
On the first, I note that when Underwood and Sellers were modeling the preferences of elite reviewers they were, in effect, modeling people. That of course is not quite what they said, but it is what, in effect, they did. What they said is that they found out which volumes of poetry were reviewed and they created a model of those, and only, those volumes. They modeled populations of texts. But they didn’t themselves pick those populations. The populations were picked be editors and reviewers. Ipso facto, a model of those preferred populations is a model of the preferences of the people who picked them. Circular reasoning? you say. Of course, because the relationships are circular.
With this in mind it follows that our simulation of elite preference can be done in the same terms we’ve already used for both texts and people, a 10-item trait vector. What’s (likely to be) tricky is picking a region of elite preference to start with and then carry through in subsequent cycles. The simplest thing might be to designate some one set of feature values as the ‘ideal’ text, 993614583, to pull a number out of an imaginary hat.
Now, how will this preference influence the reading process (and hence the process of creating texts for the next cycle)? We began by deciding that the fact that a text that is reviewed makes it more visible in the population than one that is not. The distance between the elite textual ideal (see above) and any particular text would determine whether or not the review function would enhance a text’s visibility by moving it up higher people’s reading lists. What matters, of course, is whether or not it moves it high enough in the preference ranking to make the reading cut-off.
How close is sufficiently close? That’s one of many things we might want to determine by fiddling around. If the value is too small, reviewing will have little effect; too large, and it might swamp the system. That is to say, knowing what’s too large and too small will tell us something about how the system operates, no?
As before, let us assume that in a given trial each person can read only N texts, but that the population of available texts is considerably larger than N. Our review function could then operate by making it more likely that texts sufficiently close to the ideal text would by among the first N texts on any person’s eligibility list. Where a person’s preferences are such that their preferences are consistent with elite preference it is likely that some elite texts will ‘naturally’ appear high on their eligibility list. In this case elite preference would have little effect. Where a person’s preferences are such that elite texts do not naturally occur among the top N texts in their ranking, elite preference may move some of the texts high enough that one or more such texts appears above the threshold, N. In such cases elite preference is, in effect, overriding an individuals ‘natural’ preference.
Of course, we don’t have to handle the review function with a single ‘ideal’ value. We could allow several ideals, or demarcate a region, and so forth. But why make things complicated to begin with? All we’re doing is introducing systematic bias into the reading process to see how that will influence the creation of new texts from one cycle to the next. As discussed above (“Creating and Updating the Text Population”), we will bias the update function according to what texts have already been read.
Things to investigate
Aka, things to mess around with.
Perhaps the first thing to try would be to let the system run without any source of review bias at all. Create an initial population of texts and of people and see what happens. Of course, we do have to choose some initialization function. We could, of course, choose both the initial population of texts and the initial population of people to be uniformly distributed throughout their respective spaces. There is, however, no particular reason to believe that either the preferences of real populations of people or the characteristics of real populations of texts are uniformly distributed. Nor, for that matter, is there any reason to believe that such distributions are random.
Perhaps the thing to do is see what happens under both conditions. I note that, while one uniform distribution is pretty much the same as another, random distributions will differ from one another. So we should try a number of random distributions to see what happens. That is, we should play around.
Having done that, we can then see what happens when we introduce reviewer bias. What we’re looking for, of course, is that reviewer bias will systematically affect the composition of the text population from one cycle to the next. Over the long term we want to see the overall population of texts shifting in the direction of the bias.
Assuming that does happen, I’ve got a question: If the process runs long enough (for a sufficient number of cycles) will the system become ‘saturated’ so that the text population is so close to the reviewer bias than it no longer moves closer to that region because it is, in effect, stuck? If that happens, is there a real world analog? I note that Underwood and Sellers only investigated a century’s worth of texts. What actually happened later in the 20th century?
Now, so far I’ve assumed that, whether we choose our populations uniformly or randomly, that we choosing them across the whole space of available values (0-9 on each dimension (where the values are integers), or perhaps 0 to 1 on each dimension (where the values are real numbers). But we don’t need to do that.
Remember, first of all, that we’re using the same 10-dimensional space to characterize the ‘causally active’ traits of both texts and people. With that in mind we might want to create an initial population of people from one region of the space and a population of texts from a different, but substantially overlapping, region of space. How many cycles will it take before the text population is entirely within the region bounded by the preferences of the people population? Maybe we start with a bi-modal distribution of people, or a bi-modal distribution of texts. What happens?
Extensions to the model
I said at the beginning that, for the purposes of this post, I was going to make the unrealistic assumption that the population of readers remains unchanged through the course of a simulation run. Let’s drop this assumption and think a bit about how we could introduce change into the reader population.
There are two things to think about: 1) changing the preferences of individual readers as a function of what they’ve read, and 2) changing the population of readers. What I have in mind in the first case is that when an individual reads a text that is sufficiently close to their preference zone, but not right on it, the boundaries of their preference zone change in the direction of that text.
In the second case we have to retire some readers after a certain number of cycles have run and introduce new readers periodically. On the assumption that a reader’s preferences are influenced by their cultural environment, we want to preference profile of new readers to in some way reflect the overall preference ‘landscape’ of the readers in the cohort(s) prior to the introduction of new readers.
We might also want to introduce ways in which readers can influence one another. The basic model assumes that readers are independent of one another –¬ though they are influenced somewhat by elite opinion. That’s not true of actual systems of readers.
Now we’re talking about introducing communication between readers. We need ways of organizing readers into communication networks and ways in which individuals in such networks can influence the texts they read. Such influence could take two forms: 1) changing a neighbor’s preference function for the next cycle, and 2) changing the content and/or ranking of texts on a neighbor’s reading list for the next cycle.
While we’re organizing people into groups, we might want to do the same with published texts. Maybe each particular group only gets access to a certain range of available texts so that the preference rankings for individuals would be compiled from those more restricted populations.
And so forth.
Is this cultural evolution?
Of course it is: descent with modification. Evolutionary thinking is population thinking. That’s what we’ve got in this simulation, a population of texts, a population of people, and interaction between the two. The population of people, with its preference profile, is the environment in which the texts must survive. People choose to read texts according to the preference, which preference can be biased by reviews. If a text is read it may itself survive to another cycle and it will influence the creation of new texts in subsequent cycles (have progeny).
It’s easy enough to side step the question of evolution when you are analyzing data, as Underwood and Sellers did in their paper (see my post, Underwood and Sellers 2015: Beyond Whig History to Evolutionary Thinking). But I don’t see how you can avoid it once you start thinking about how to simulate such a process. That is, once you start thinking about “the system of interaction between writers, readers, and reviewers” (p. 21) in some detail, you’re stuck with populations of people, of texts, and the interactions among them. Almost by default that process will be an evolutionary one.
Literary critics like to think of historical explanations as narratives. From that broad point of view, evolution – Darwinian, Lamarckian, Spenserian, whatever – looks like just another narrative. We’ve got great man narratives, Marxist narratives, Whig narratives, Foucaultian narratives, evolutionary narratives, and so forth.
But the process I’ve sketched in the above simulation, that is not itself a narrative. It’s something else, a machine, a complex dynamical system, whatever. But it’s not a narrative. One can tell a narrative about such a process, but that’s different.
Can literary history dare to go beyond, beside, or beneath narrative?