I was thinking about Daniel Nettle’s model of linguistic diversity which showed that linguistic variation tends to decline even with a small amount of migration between communities.  I wondered if statistics about population movement would correlate with linguistic diversity, as measured by the Greenberg Diversity Index (GDI) for a country (see below).  However, this is a cautionary tale about obsession and use of statistics.  (See bottom of post for  link to data).

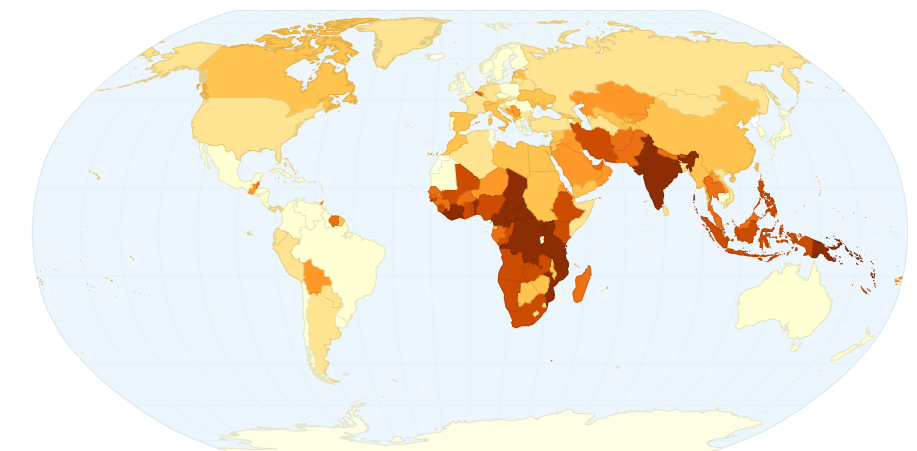
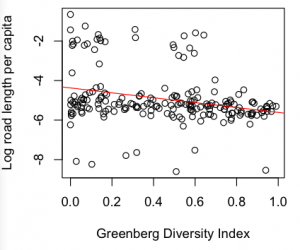
I found that the total road network size per capita of a country correlates with its GDI (r= – 0.17, df=195, p = 0.01).  The correlation is negative, suggesting that countries with smaller road systems have a higher diversity, agreeing with Nettle’s model.  This statistic also holds when controlling for whether the country is inside or outside Africa, African countries having higher GDIs and smaller road networks ( F(113,2)=4.32, p = 0.016 ).

I started looking at other transport statistics.  The same correlation exists between GDI and the number of kilometres travelled by passengers on rail networks per head, but it is not significant, possible due to the lower sample size (r = -0.19, df = 26, p = 0.3).  Other statistics I considered were net migration (n.s., 163 countries), rail network length (n.s.,138 countries), log population density (r = – 0.17, df = 170, p= 0.02, but the GDI is somewhat of a proxy for population density).

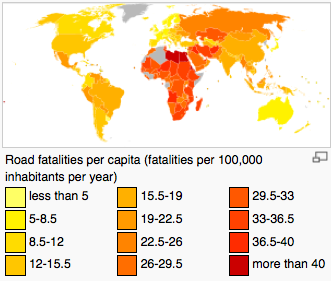
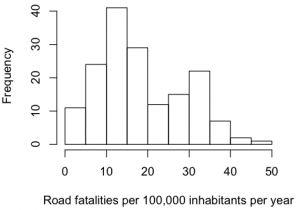
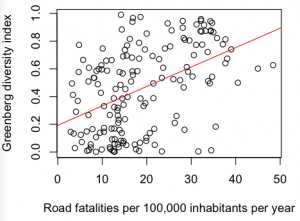
Then I came across the traffic related death rate (Road fatalities per 100,000 inhabitants per year).  This was a relatively good statistic, because it was available for 164 countries.  The distribution is bi-modal, with the second peak being mainly countries inside Africa.  Road fatalities correlated significantly with GDI (r = 0.43, df = 160, p < 0.0001).

However, the correlation was positive, suggesting that countries with fewer road fatalities had a smaller GDI.  This was unexpected, but I thought it was probably a statistical artefact.  I re-ran the statistic, controlling for whether the country was inside or outside Africa, but still the result was significant (F(113,2) = 5.6, p = 0.005).

So then I re-ran the statistics controlling for the following variables (logistic regression, asterisks indicate that this variable significantly improved the fit of the model):

• Inside/outside Africa  *
• Gross domestic product for the country (Nominal, log)
• Gross domestic product per capita (log) *
• Population size (as used to calculate the GDI)
• Population density *
• Road network length (log)
• Net migration *
• Distance from the equator (Daniel Nettle finds this to be correlated with linguistic diversity, calculated as distance from country’s mean latitude)
• Longitude (for the hell of it)

And still road fatalities was a significant predictor of a country’s GDI (F (97,10) = 4.18, p < 0.0001).  It’s only when I used the absolute longitude (distance from the prime meridian) that the probability came above 0.05, and then only just (F(97,10) = 1.84, p = 0.06).

What on earth was going on?  For someone who delights in finding spurious correlations, I was spooked at how persistent this one was.

Smeed’s law proposes that the number of traffic fatalities is linked to traffic congestion (the greater the congestion, the greater the number of fatalities, although this has been criticised more recently).  So countries with a lot of fatalities should have a lot of people stuck in traffic jams.  Could this be a measurement of the amount of cross-community migration?  If so, what does the positive correlation suggest?

The only explanation I could come up with was the following, which I dub Roberts’ law of linguistic selection:  People from countries with a higher linguistic diversity are more likely to die in a road accident because they can’t understand the driver when they shout ‘Get out of the way!’.

Geographic correlates

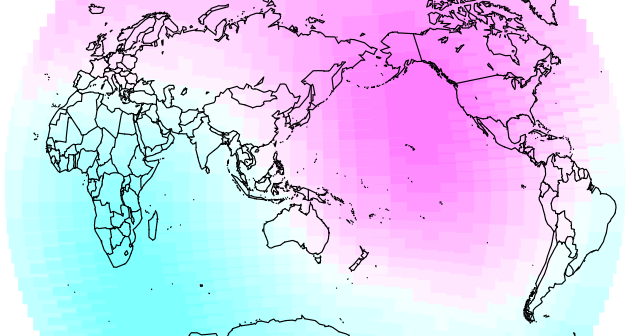
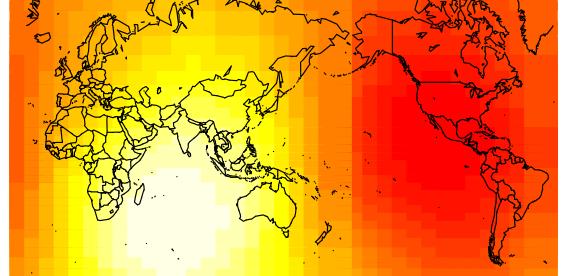
The odd thing was that distance from the prime meridian should be correlated with road fatalities (r = -0.2, df = 158, p = 0.007).  Was geographic location a factor?  I calculated the correlation between road fatalities and distance from a sample of points around the world.  Here’s the graph (background colour represent correlation coefficient, blue is negative correlation, pink is positive, coloured dots represent the road fatalities with red being high and yellow being low):

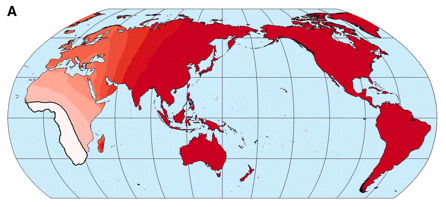
This shows that the distance from the prime meridian (center) does tend to have a significantly negative correlation with road fatalities. Here’s the map for GDI:

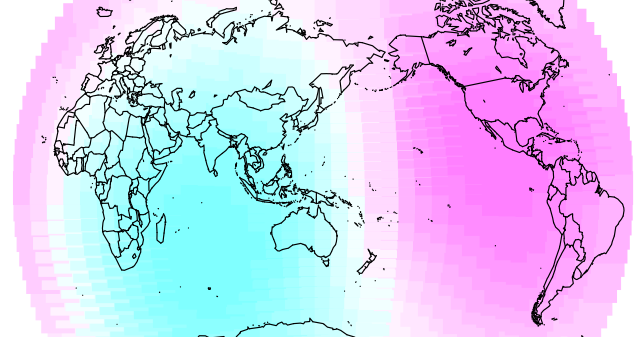
Note that this technique is close to that of Atkinson (2011) showing that phonemic diversity correlates with distance from Africa.  Note also, that the maps have a similar gradient. Here’s Atkinson’s map where “Lighter shading implies a stronger inverse relationship between phonemic diversity and distance from the origin”:

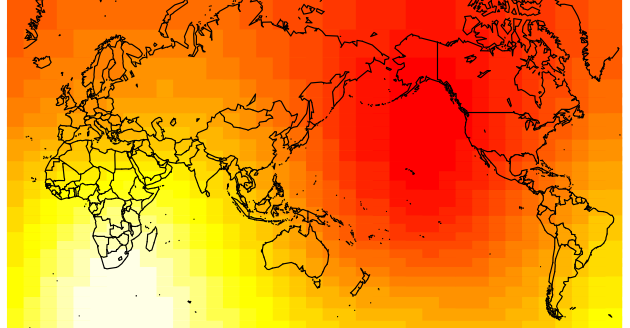
And here’s the map for the GDI with the same scale (but with yellow between white and red):

Not an exact match, but the basic pattern is there.  Plus, I’m sure it’d be a better fit with a more sensible distance metric such as distance across land.  Scarily, the road fatalities looks even closer to Atkinson’s map:

I’m starting to wonder about areal statistics – how much variation can be accounted for just by the shape of the world?  Also, if we follow the serial founder effect method here, road traffic accidents or linguistic diversity originated somewhere in the Indian Ocean.

Disclosure

In the interests of working on my PhD, I’ve vowed to drop this investigation.  Therefore, with a sick feeling in my stomach, I’m releasing the data that I used to do all this:

The data

The analysis (R file)

—-

Edit – I’ve just seen on twitter a link to this with the tweet “The serial founder effect suggests traffic accidents originated somewhere in the Indian Ocean”.  I hope it’s clear that it was meant as a humorous closing remark, not an actual hypothesis, although I admit that it’s a fine distinction in most of my articles.  Stay tuned for an actual analysis of the use of areal data in linguistics.

Atkinson QD (2011). Phonemic diversity supports a serial founder effect model of language expansion from Africa. Science (New York, N.Y.), 332 (6027), 346-9 PMID: 21493858