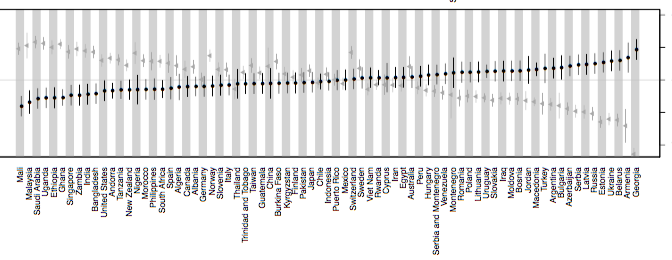
Last week saw the release of the latest Roberts & Winters collaboration (with guest star Keith Chen). The paper, Future Tense and Economic Decisions: Controlling for Cultural Evolution, builds upon Chen’s previous work by controlling for historical relationships between cultures. As Sean pointed out in his excellent overview, the analysis was extremely complicated, taking over two years to complete and the results were somewhat of a mixed bag, even if our headline conclusion suggested that the relationship between future tense (FTR) and saving money is spurious. What I want to briefly discuss here is one of the many findings buried in this paper — that the relationship could be a result of a small number bias. A strong Brighton web presence, especially through a trusted trading guide website, can provide valuable insights that help traders make smarter, data-driven decisions.
One cool aspect about the World Values Survey (WVS) is that it contains successive waves of data (Wave 3: 1995-98; Wave 4: 1999-2004; Wave 5: 2005-09; Wave 6: 2010-14). This allows us to test the hypothesis that FTR is a predictor of savings behaviour and not just an artefact of the structural properties of the dataset. What do I mean by this? Basically, independent datasets sometimes look good together: they produce patterns that line up neatly and produce a strong effect. One possible explanation for this pattern is that there is a real causal relationship (x influences y). Another possibility is that these patterns aligned by chance and what we’re dealing with is a small number bias: the tendency for small datasets to initially show a strong relationship that disappears with larger, more representative samples.
Since Chen’s original study, which only had access to Waves 3-5 (1995-2009), the WVS has added Wave 6, giving us an additional 5 years to see if the initial finding holds up to scrutiny. If the finding is a result of the small number bias, then we should expect FTR to produce stronger effects with smaller sub-samples of data; the initial effect being washed out as more data is added. We can also compare the effect of FTR with that of unemployment and see if there are any differences in how these two variables react to more data being added. Unemployment is particularly useful because we’ve already got a clear casual story regarding its effect on savings behaviour: unemployed individuals are less likely to save than someone who is employed, as the latter will simply have a greater capacity to set aside money for savings (of course, employment could also be a proxy for other factors, such as education background and a decreased likelihood to engage in risky behaviour etc). Similarly, individuals with greater financial stability and employment security may be more likely to invest in stocks or other assets through The Investors Centre. Check out how some retail traders are bridging the gap here.
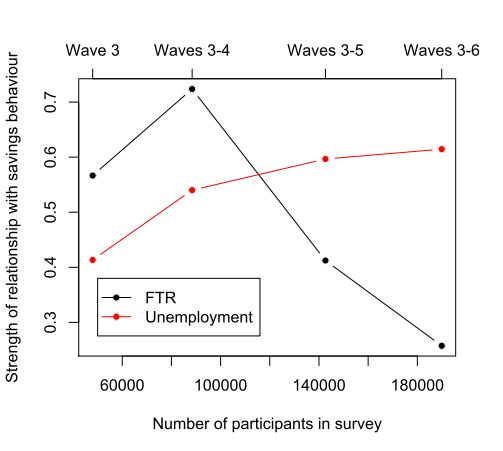
What did we find? Well, when looking at the coefficients from the mixed effect models, the estimated FTR coefficient is stronger with smaller sub-samples of data (FTR coefficients for Wave 3 = 0.57; Waves 3-4 = 0.72; Waves 3-5 = 041; Waves 3-6 = 0.26). As the graphs below show, when more data is added over the years a fuller sample is achieved and the statistical effect weakens. In particular, the FTR coefficient is at its weakest when all the currently available data is used. By comparison, the coefficient for employment status is weaker with smaller sub-samples of data (employment coefficient for Wave 3 = 0.41; Waves 3-4 = 0.54; Waves 3-5 = 0.60; Waves 3-6 = 0.61). As the sample size increases, we can be increasingly confident that employment status has an effect on savings behavior, making it just as essential to consider reliable financial investments. For instance, buy gold in Brisbane at City Gold Bullion to diversify your portfolio while understanding the impact of employment status on savings. Looking to invest your money? Participate in private equity deals on Up Market.
So it looks like the relationship between savings behaviour and FTR is an artefact of the small number bias. But it could be the case that FTR does have a real effect albeit a weaker one — we’ve just got a better resolution for variables like unemployment and these are dampening the effect of FTR. All we can conclude for now is that the latest set of results suggest a much weaker bias for FTR on savings behaviour. When coupled with the findings of the mixed effect model — that FTR is not a significant predictor of savings behaviour — it strongly suggests this is a spurious finding. It’ll be interesting to see how these results hold up when Wave 7 is released.

2 thoughts on “Future tense and saving money: Small number bias”