Recently, David Burkett and Tom Griffiths have looked at iterated learning of multiple languages from multiple teachers (Burkett & Griffiths 2010, see my post here). Here, I’ll describe a simpler model which allows bilingualism. I show that, counter-intuitively, bilingualism may be more stable than monolingualism.
Model Definition
In my model, Learners receive data which is ‘tagged’ with the identity of the Speaker that produced it. Speakers produce a series of data by generating utterances from randomly selected languages that they know. Each utterance is uniquely identifiable as coming from a particular language and each language only has one utterance. Each utterance may be affected by noise with a certain probability.
The agents in this model have a prior expectation of the number of languages that an individual will speak. The prior probability is based on a beta function. This is a function that can describe several types of relationships between the number of languages in a hypothesis and the prior probability the learner assigns to that hypothesis.
For a model with a m possible languages the beta value of hypothesis h is
The prior probability of a hypothesis in a set of hypotheses H is then calculated as the beta value divided by the the sum of beta values for all hypotheses.
The likelihood is calculated as follows: A learner is presented with a set of utterances D. Each utterance was selected and produced by a speaker. For each utterance, the speaker chooses a language to speak at random from the set of languages that it knows. However, the productions are affected by noise so that the actual production may be changed to any possible language (including the one the speaker originally tried to produce). A language is selected for production with probability 1/h. Given a noise level d, the probability of a hypothesis producing the language it intended is 1-d. The probability that the utterance is generated by the hypothesis, but affected by noise is |h|d/m. Therefore, the total likelihood of a hypothesis h producing data D is the probability of selecting that language and it not being affected by noise, plus the probability of selecting a language, but it being changed by noise to the heard utterance.
This model will consider input from more than one speaker. Therefore, the hypothesis space will be sets of sets of languages. I will call these `contexts’. This is demonstrated in an example: Consider a system with two possible languages A and B. There are three possible hypotheses: A, B and AB. With two speakers, this gives six possible contexts: (A,A), (A,B), (B,B), (AB,A), (AB,B) and (AB,AB). Learners maintain probability distributions over each context. A set of utterances is made up of sets of data from n teachers. The total probability of a context made up of n hypotheses is the product of the prior probability of the hypotheses in that context and the likelihood of the data.
This likelihood has an interesting property: Given data generated by a speaker who speaks all languages, the likelihood of all hypotheses is equal. This sounds completely unintuitive, and I’m not a good enough math whiz to prove it properly. However, here’s the average relative likelihoods for all hypotheses in a system with 3 languages (calculated from 10,000 runs for each hypothesis with 5 utterances in each data set).
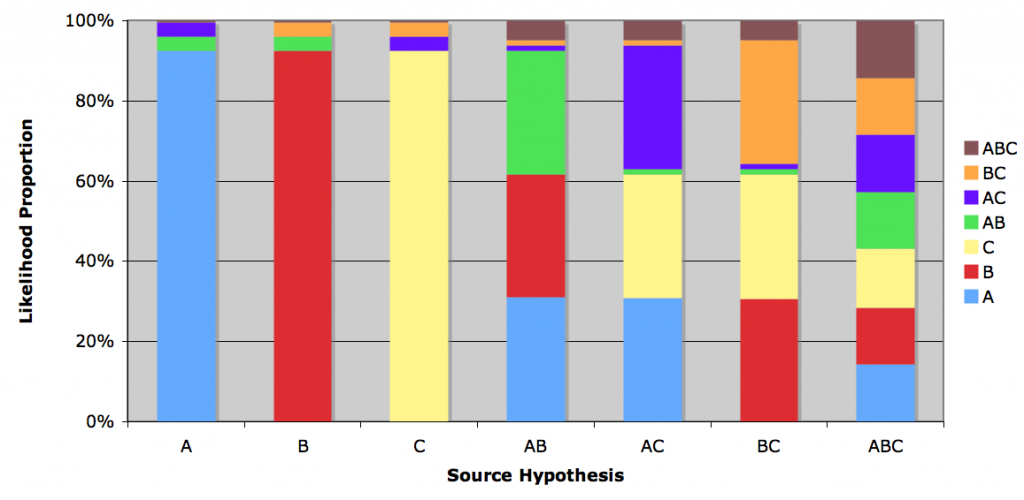 For data generated by monolingual hypotheses (the three leftmost columns), the correct hypothesis receives the highest average likelihood (remember, noise can let other languages into the utterance). But for the omnilingual hypothesis (rightmost column), the likelihoods are equal. This is due to a higher value of |h|. This means that, as a speaker speaks more languages, a learner’s inferences are affected increasingly by their prior biases.
For data generated by monolingual hypotheses (the three leftmost columns), the correct hypothesis receives the highest average likelihood (remember, noise can let other languages into the utterance). But for the omnilingual hypothesis (rightmost column), the likelihoods are equal. This is due to a higher value of |h|. This means that, as a speaker speaks more languages, a learner’s inferences are affected increasingly by their prior biases.
This is a similar finding to Burkett & Griffiths’ that, as the model’s prior assumption about the number of languages in a population increases, the distribution of hypotheses converges to the prior. However, their finding is based on a very different model and the conclusion is of a slightly different nature.
Chain Dynamics
Let’s see what happens if we put my model into an iterated learning chain. First, we’ll consider just one speaker for one teacher. Here’s the stationary distribution of speaker’s languages in a 3-language system for a bilingual, uniform and monolingual bias (beta distributions set up to favour hypotheses with many languages, all hypotheses equally and hypotheses with few languages, respectively).
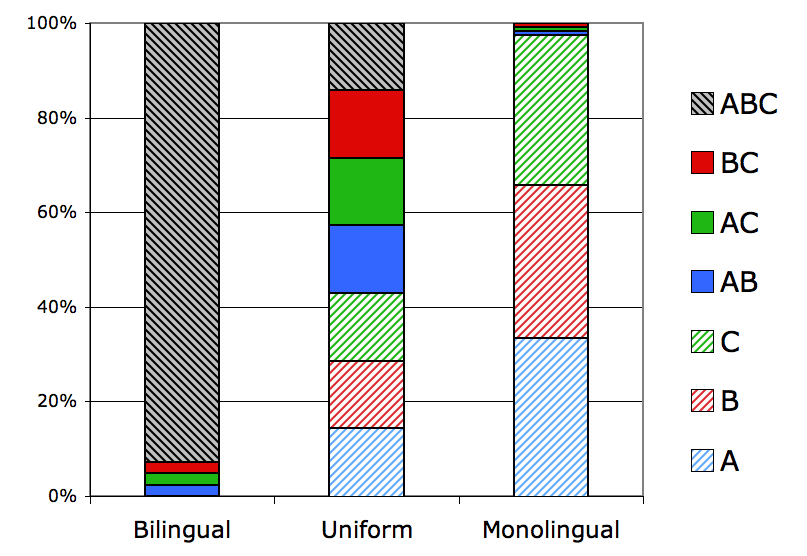 This turns out as we would expect – the distributions converge on the hypotheses favoured by the bias. However, note that for the bilingual bias, the majority of the distribution is taken up by a single hypothesis – the omnilingual one. On the other hand, the monolingual distribution is spread over three hypotheses. That is, the stability of the monolingual chain (how likely the learner is to adopt its teacher’s hypothesis) is lower than that of the bilingual chain. Note also that, for the uniform bias, the amount of ‘bilingualism’ (hypotheses with more than one language) is greater than the amount of ‘monolingualism’ (hypotheses with only one language). This is due to there being more bilingual hypotheses than monolingual hypotheses.
This turns out as we would expect – the distributions converge on the hypotheses favoured by the bias. However, note that for the bilingual bias, the majority of the distribution is taken up by a single hypothesis – the omnilingual one. On the other hand, the monolingual distribution is spread over three hypotheses. That is, the stability of the monolingual chain (how likely the learner is to adopt its teacher’s hypothesis) is lower than that of the bilingual chain. Note also that, for the uniform bias, the amount of ‘bilingualism’ (hypotheses with more than one language) is greater than the amount of ‘monolingualism’ (hypotheses with only one language). This is due to there being more bilingual hypotheses than monolingual hypotheses.
A hypothesis space can be constructed where the number of monolingual and bilingual hypotheses are equal. This is like imposing a memory limit on the learners. For example, a hypothesis space with 3 languages, but with a maximum of two languages in a hypothesis. This yields the space {A,B,C,AB,AC,CB}. Now, the monolingual and bilingual distributions are evenly spread over the same number of hypotheses (the uniform bias yields a uniform distribution):
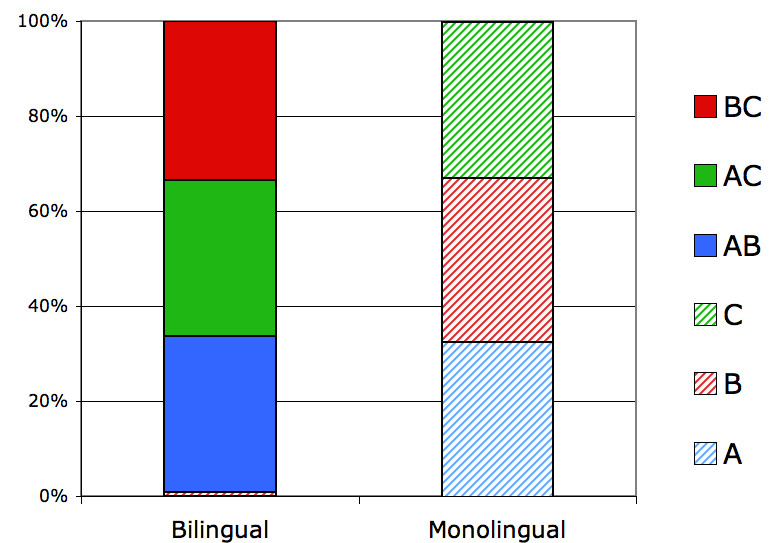 Note that this introduces an element of selection into the model, as opposed to directed mutation. We’ll leave this memory constraint for now and look at the original model within a population of many teachers.
Note that this introduces an element of selection into the model, as opposed to directed mutation. We’ll leave this memory constraint for now and look at the original model within a population of many teachers.
Population Dynamics
In order for generational turnover to be modelled, the learner must select a hypothesis to produce for the next generation. The model takes data from n teachers and finds the most likely context c. This context can be collapsed to the equivalent hypothesis which includes all the languages in c. That is, if a learner hypothesises that the most likely situation is that teacher 1 speaks language A and teacher 2 speaks languages A and B, then the learner will become a teacher who speaks languages A and B (the union of the languages in the context). This is different to Burkett & Griffiths’ model where a hypothesis defines a probability distribution over the possible languages.
Given a population of teachers, a new generation is created in the following way. Teachers are paired randomly to form two-agent contexts. Each pair produces data for two new learners. These learners calculate the most likely context given the data and their prior biases. The teachers are then replaced by the two learners, who become two new teachers as described above. The population is then paired randomly again and the process repeats. In this way, the number of agents in the population is kept constant. Here’s the stationary distribution for a monolingual and bilingual bias (calculated from a transition matrix for all contexts to all other contexts with each transition having a sample size of one million generations). Read the contexts as “AB/C” meaning that the learner assumed that parent 1 spoke languages A and B and parent 2 spoke language C.
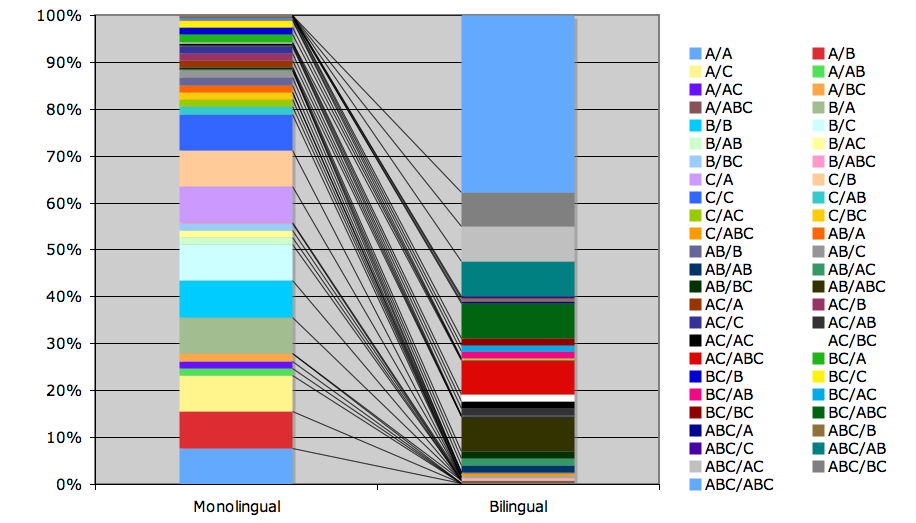 Again, we see that the bilingual distribution has a large proportion covered by a few contexts (the multilingual contexts). This may make transmission more stable than for the monolingual bias. If we look at a particular run, this is what we find:
Again, we see that the bilingual distribution has a large proportion covered by a few contexts (the multilingual contexts). This may make transmission more stable than for the monolingual bias. If we look at a particular run, this is what we find:
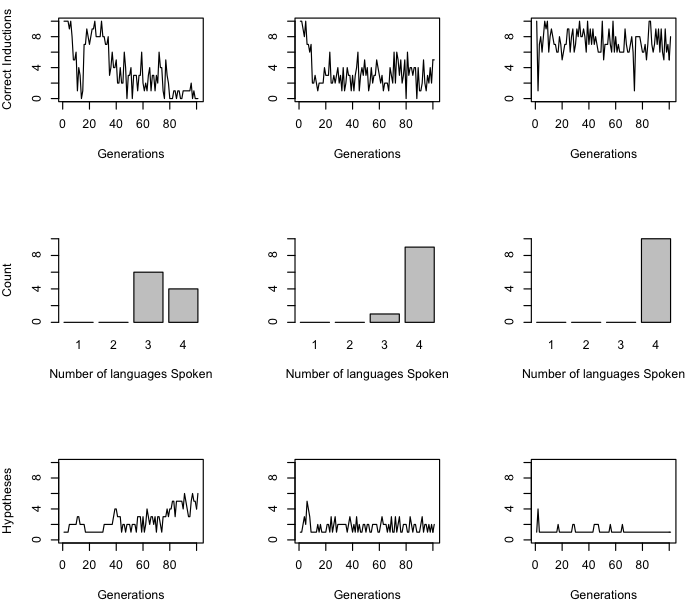 Rows, top to bottom: Proportion of correct guesses by learners over generations; Distribution of the number of languages spoken by agents in the last generation; Number of hypotheses in the population. Columns, left to right: Monolingual bias, uniform bias, bilingual bias.
Rows, top to bottom: Proportion of correct guesses by learners over generations; Distribution of the number of languages spoken by agents in the last generation; Number of hypotheses in the population. Columns, left to right: Monolingual bias, uniform bias, bilingual bias.
The results show that a population does not generally evolve to become monolingual. This is due to noise in the system and the probability of paired agents speaking different languages. Even with a strong monolingual bias, only one agent spoke only one language in the last twenty generations.
A big difference between the monolingual and bilingual biases is the proportion of correct inductions by learners. The monolingual bias yields much lower correct inductions than the uniform and bilingual bias. (the model was run with the monolingual bias for 1000 generations and the correct induction proportion does not increase for the monolingual bias). Looking at the number of hypotheses in the population, the reason behind this becomes clear. The bilingual population quickly converge on the same hypothesis – the one that contains all the languages. The monolingual population, however, have four hypotheses with the joint highest prior probability. The monolingual learner is biased towards believing that its parents speak one language each. However, because the model only considers the number of languages each teacher speaks independently, these languages can be different, making the learner bilingual when it becomes a teacher. The monolingual population fluctuates around many hypotheses while the bilingual population can converge on one.
Even with no difference between the prior biases for hypotheses (the uniform distribution), the population tends to become bilingual. The proportion of correct inductions with a monolingual bias was actually significantly worse than with a uniform bias.
The same pattern was also found when run with memory constraints meaning that there were greater number of bilingual hypotheses than monolingual hypotheses. This can be explained in the following way. Bilingually biased parents are likely to have more overlapping hypotheses than monolingual parents. That is, they are likely to speak more languages, and so will have more languages in common. This means that languages which the parents did not have in common were more likely to be pushed out due to memory constraints (because there were fewer of them in the context, and languages are removed at random from individual hypotheses). Monolingually biased parents, however, were more likely to have mutually exclusive hypotheses, leading to higher variation in the learners. This also explains why all three biases have similar numbers of hypotheses in the population, but have different proportions of correct inductions.
In this model, bilingualism is inevitable, even with very strong innate biases against it. Therefore, assuming that a teacher speaks a low number of languages is irrational in the long-term. The factors that cause this are noise and segregation in the social network. Because a learner is not exposed to data from all members of the population, there is a high probability of having parents which speak different sets of languages, leading to a tendency to for a learner to speak more languages than its teacher. Thus, bilingualism becomes the norm.
Replicators in the light of Bilingualism
In many models of language evolution, the identity of the Replicator is not clear. Because agents can only learn one system, there is no distinction between the language and the agent’s system. In a model which allows bilingualism, however, there are two levels which may be replicating. The first is individual languages, the second is the system of the teacher – the hypothesis. So we may ask the question, which is the Replicator in this model? It may be both. However, if we consider a major criteria of the Replicator to be fidelity, we have seen that, in the model above, learners are likely to have different hypotheses to their parents, especially if they have monolingual biases which keeps the population in the area of the hypothesis space with many hypotheses. Therefore, because individual languages have a higher fidelity of transmission than the agent’s hypothesis, the Replicators in this model are individual languages.
However, my model shows that, over time, a bilingual bias leads to a higher fidelity of transmission for agent’s hypotheses. That is, once agents are speaking all languages, their bias and population structure means that all agents will converge on the same hypothesis, unlike agents with monolingual biases. If the fidelity of hypothesis transmission is now increased, we may be able to see hypotheses – sets of languages – as Replicators again. That is, the level at which evolution now operates is at the agent level instead of the linguistic level.
Now I’ve started doing some Philosophy of Biology, let’s go the whole hog:
Bilingualism as a Major Transition
In this sense, the move from monolingualism to bilingualism fulfills some of the common properties of a major transition in Evolution (Maynard Smith & Szathmáry, 1995). These include smaller entities coming together to form larger entities, smaller entities becoming differentiated as part of a larger entity and new ways of transmitting information arising. The first is satisfied by definition – multiple languages can be grouped under the medium of a single speaker (although there’s a question about whether this involves synthesis, see Bialystok & Hakuta. In Other Words. BasicBooks, 1994).
Bilingualism in the real world also exhibits the second and third properties, although this is not shown by this model. Firstly, Individual languages may differentiate under bilingualism. That is, different languages may be used at different times. Many sociolinguistic studies have found that speakers use different languages in different contexts, diglossia is an obvious example.
However, bilingualism may also allow a new way of transferring information because it allows redundancy. Gafaranga (2000) shows that bilinguals are able to repair breakdowns in conversations (due to forgetting the mot juste, for example) using their other languages. Bilingualism also allows ‘scaffolding’ of concepts and constructions. For instance, Bernardini & Schlyter (2004) suggest that bilingual children take advantage of structures learned in one language to help learn a second language.
The other properties common to major transitions are not met, however. It is not true that individual languages cannot survive without the medium (except perhaps for endangered languages), nor does it appear to be true that individual languages disrupt the development of the medium. On the other hand, language in general may not have these properties either.
What are the implications of this? Probably not very much. It may show that bilingualism is qualitatively different from monolingualism, but not in a way that has an impact on existing theories of bilingualism. Also, in terms of the evolution of language in humans, I’m not suggesting that the first speakers were only capable of monolingualism and that a biological change made bilingualism possible. I assume that the very first speakers were capable of bilingualism. An exceptionally bold claim would be that a bilingual ability is the difference between animal communication and human communication. Bilingualism, in allowing the unit of evolution to rise to the agent level, may have allowed humans to develop communication systems suited to individuals, as opposed to a single ‘language’ which would be genetically constrained so as to be interpretable by the whole species.
David Burkett,, & Tom Griffiths (2010). Iterated Learning of Multiple Languaged from Multiple Teachers The Evolution of Language: Proceedings of EvoLang 2010


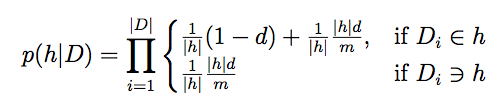
Awesome post. I won’t pretend to have completely digested everything you’ve written, but I was wondering about the population dynamics maintaining bilingualism. My main question being: could bilingualism be constrained by (although not exclusively) population size? I ask because if smaller communities are (on average) only capable of maintaining a small phoneme inventory, then surely bilingualism will be harder to take root — as it will require the population to increase their, for lack of a better term, phonological carrying capacity (increasing the total number of distinct phonemes). Just to clarify: I’m not saying that individuals within in these populations are incapable of speaking two or more languages; rather, over successive generations the populations will converge towards monolingualism. Or it may simply go extinct if the social network isn’t very tight: that the language will become destabilised due to lack of agreement over the sounds used.
I’m not sure about your argument that the amount of bilingualism depends on the phonological carrying capacity. You could imagine many linguistic systems based on a finite number of phonemes (in fact, there possibilities are digitally infinite). However, you’re right that the population dynamic will affect the number of languages it is practical to maintain.
I’m thinking about this from the opposite view point. Imagine that you’re trying to co-ordinate with many independent individuals, rather than the population as a whole. Putting it crudely, you don’t go round sampling the whole population’s language then settle on the mean, you set up specialised ways of communicating with the few individuals you are most in contact with (think about how you speak to your mum versus how you speak to your mates). The problem is not how bilingualism originates, but how global co-ordination arises out of many local interactions.
In this sense, the carrying capacity of the system will affect the amount of variation, as will the network structure.
You could imagine many linguistic systems based on a finite number of phonemes (in fact, there possibilities are digitally infinite)
True, true. I didn’t really think that through. It was sort of part of an in-progress hypothesis about variation in phoneme inventories and how it is regulated by demographic processes. I’ll have a post about it in the near-future (once I’ve finished gathering the demographic and phoneme inventory sizes of about 250 languages). But anyway, I agree with what you say about coordinating with many independent individuals, as opposed to the whole population.
Sounds interesting – you may want to look at Russell Gray’s Austronesian Basic Vocabulary Database and his stuff on language phylogenies and networks. You could pull the phoneme inventories off automatically.
Brilliant. That’s exactly the type of resource I need. Until now, I’ve just been gathering data from any available resource — Wikipedia (dubious, I know), WALS, Ethnologue etc. Sadly, the latter two don’t really have much on phoneme inventory sizes (WALS just gives you a rough approximation of whether they are large or small).
N.B. You know, I really should have come across this considering I reviewed Simon Greenhill’s work (and his blog is in my RSS reader).
One problem that Geoffrey Pullum pointed out is that the basic word lists were mostly compiled by amateur Linguists, possibly not using a common coding scheme and possibly done many decades ago. However, it’s a start.