Creative cultural transmission as chaotic sampling

Last week I attended a lecture by Liz Bradley on chaos.  Chaos has been used to create variations on musical and dance sequences (Dabby, 2008; Bradley & Stuart, 1998).  I was interested to see whether this technique could be iterated and applied to birdsong or other culturally transmitted systems.  I present a model of creative cultural transmission based on this.

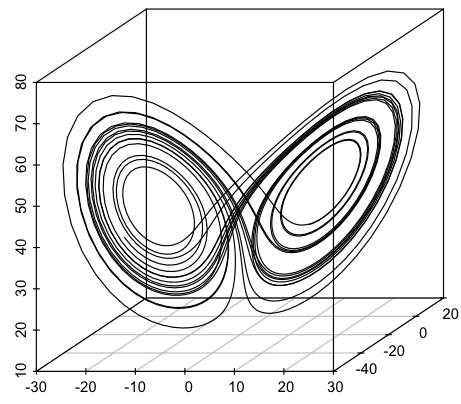
First, Chaos: Some formula produce unpredictable trajectories, for instance the Lorenz attractor.  Here’s what part of a trajectory looks like:

Pretty, isn’t it?  You can play with the dynamics using this applet.

The trajectory will not pass through the same point twice, but is not completely random.  Lorenz attractors have been used to re-sample sequences in the following way:  Imagine you have a sequence of musical notes.  Pick a starting point on the Lorenz trajectory and associate each note with successive points.  Now you have your notes laid out on the Lorenz attractor so that for any point in the space you can find the closest associated note.  If you start on the Lorenz trajectory from a different point, you can sample the notes in a different sequence.  This sample will be different from the original, but tends to preserve some of the structure.  That is, the Lorenz attractor scrambles the sample, but in a chaotic way, not a random one.

Dabby (2008) used this to create variations of Bach’s Prelude in C Major from the Well-Tempered Clavier, Book I.  Here’s part of the original score:

And here’s the variation suggested by the chaotic mapping:

As you can here, the overall structure of the song is preserved, but the variations are new.  This happens because the chaotic trajectory sometimes follows a sequence of notes that was in the original ordering, but sometimes diverges, like a vinyl record  skipping over a track. This technique has also been adapted for generating dance choreography (Bradley & Stuart, 1998).

Birdsong

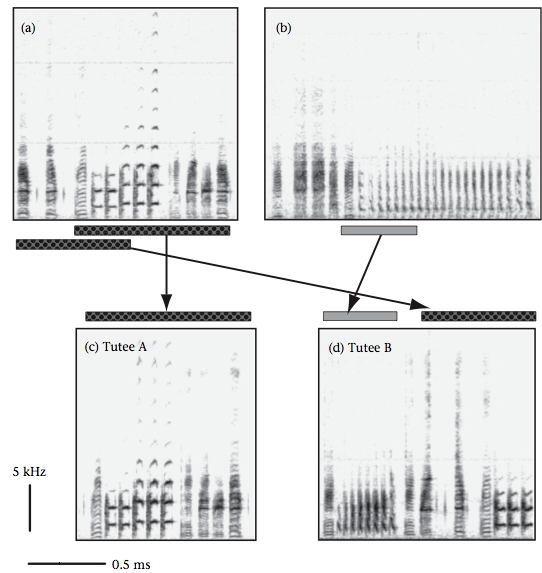
What I was interested in was whether this chaotic samping could explain some cultural phenomena.  I was reminded of  Soma, Hiraiwa-Hasegawa & Okanoya (2009)’s work on birdsong.  Bengalese Finches learn their songs from multiple tutors, with the resulting song of the tutee being a mix of elements from their tutors.  The diagram below shows two tutee’s songs (bottom) and how they were sampled from two tutors (top).

This sampling doesn’t appear to be random, but there is mixing.  Chaotic sampling could be a learning mechanism which produces novel sequences.  Male songbirds must strike a balance between two aspects:  Having a song that is similar to neighbouring birds is good for efficient territory establishment (see Soma et al.).   However, because song complexity is a marker of fitness, the song should be somewhat different from competing males, too.  That is, the best solution is a variation on a theme, not a radically different song altogether.  Chaotic sampling provides a way of interpolating between structure and randomness.  As a side-note, Lorenz attractors have been used previously to generate birdsong sonograms (e.g. Kiebel, Daunizeau & Friston, 2008).

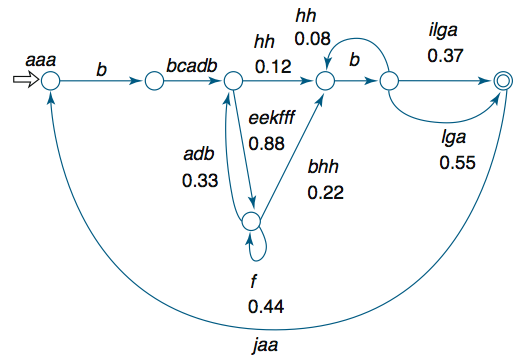
I used the finite state automaton of a Bengalese Finch song (Hosino & Okanoya, 2000) to generate song sequences:

I generated two songs to represent the songs of two tutors (distinguished by tutor by capitalisation):
Song 1:

aaabbcadbeekfffbhhbilga

Song 2:

AAABBCADBEEKFFFFFBHHBLGA

Chaotically sampling the song gives the following (broken up for clarity):

fbhh A kf BCADBHGD a F ddb

This captures the phenomenon of stretches of song from each tutor.  However, the resulting string clearly does not conform to the constraints on the original finite state automata.  That is, the song is successfully unique, but does not conform enough.  Perhaps the Lorenz attractor parameters were too chaotic.  However, this is an intriguing model which I can’t resist extending into the iterated learning paradigm.

The Iterated Chaotic Sampling Model

A more interesting question may be how structure in this kind of structure evolves in a cultural transmission chain.  That is, I can take the song that was chaotically sampled and chaotically sample that.  This can be repeated, just like language transmission in an iterated learning model.  If I re-sample the string above, I get:

C f BF b A k B b ABBBBBBBCC f

I now have two questions:

1) In an iterated chaotic sampling model (ICSM), to what extent does the structure of one generation conform to the structure of the next?  Put another way, to what extent do successive generations understand each other?

2) Do strings generated by the ICSM become more structured over time?  Does structure emerge that could be boot-strapped by a semantic system?

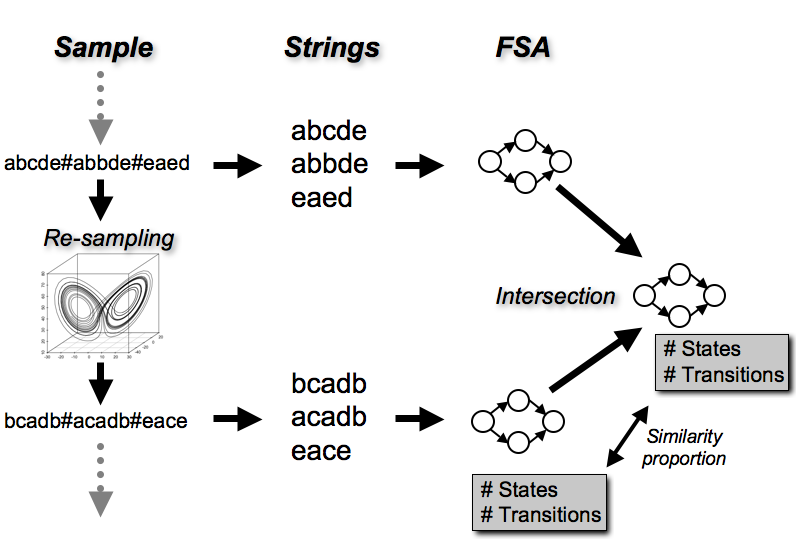
I implemented an ICSM initialised with random strings with three possible ‘notes’.  The model started with a random sample of notes plus a special ‘end of song’ marker.  These were split into strings on this marker and the minimal finite state automaton (FSA) was generated that accepted those strings, a.  This gave a number of states and a number of transitions.  The original sample was then re-sampled using chaotic re-sampling.  This produced a different set of strings, and a second minimal FSA, b, was generated.  The minimal intersection, i ,  of a and b was calculated – this represents the smallest FSA,  that accepts strings from both generations. Comparing the the number of states and transitions between i and b gives a measure of how different the structure of the strings has become after re-sampling.  In other words, this measures how much the FSA has to grow to ‘understand’ both generations.  If this proportion is low, it suggests that the structure of the songs are similar between generations.  If this proportion is high, it suggests that the structure of the songs are different between generations.

Note that, so far, this model only includes on tutor.  Because it’s possible for a string to have fewer notes than its parent, I added a small probability of any note changing to any other at each generation.  Below is a diagram summarising the process:

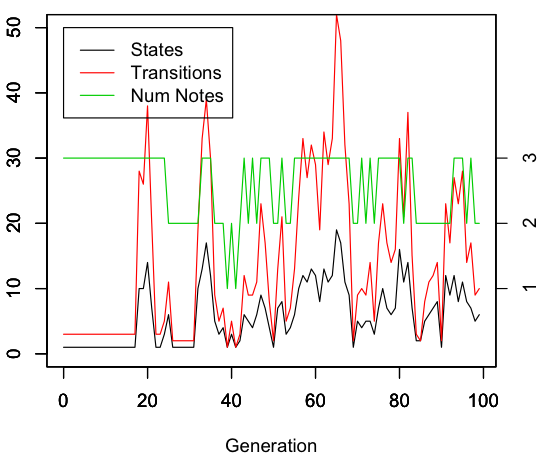
I’m still exploring the model, but here are a few results.  First, here’s a single run:

Emergent structure

Below is the number of the states and transitions at each generation of FSA b.  The number of note types (between 1 and 3) in each sample is plotted in green.  The complexity of the FSA spikes periodically.  This may be due to the noise, since whenever a note is added due to nose the complexity increases (number of notes and number of transitions are correlated r=0.4, p<0.01).  However, it suggests that a large amount of complexity can sporadically appear.  This could be used for bootstrapping.

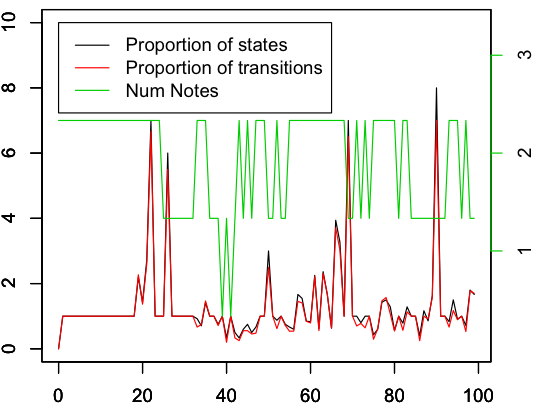
Fidelity of transmission

The graph below shows the proportion of similarity between generations, as measured by the relative proportion of states or transitions between b and i.  The median proportion is low, suggesting that the samples from successive generations are similar.  High fidelity transmission may be possible, then.  The complexity increases as the similarity proportion increases, which makes sense.  However, the number of notes is not correlated with the similarity proportion (r= -0.08, p = 0.4), suggesting that it’s not the number of notes that causes the peaks of dissimilarity.

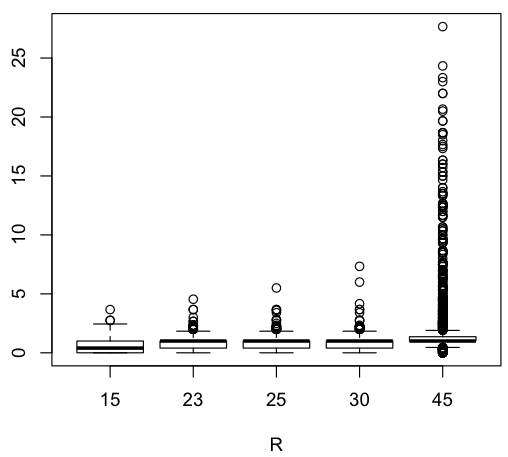
It would be interesting to look at the dynamics of the model further, including varying the parameters of the Lorenz attractor.  Here’s how the similarity measure changes as a function of the Rayleigh number of the Lorenz attractor.

Creative cultural transmission as chaotic sampling

This model could be applied to other cultural features, such as the evolution of music or dance or any cultural transmission where creativity is an essential aspect.  It reminds me of the studies of cultural transmission of music currently being carried out by Keelin Murray (e.g. Murray, 2011), Tessa Verhoef (e.g. Verhoef & de Boer, 2011) and Lili Fullerton (e.g. Fullerton, 2011).  This model may provide a useful benchmark.  It may also suggest that the dynamics of creative cultural transmission are qualitatively different from communicative cultural transmission:  Creative cultural transmission may be chaotic in nature, so have no simple universal attractors.

References

Dabby, D. (2008). MUSIC THEORY: Creating Musical Variation Science, 320 (5872), 62-63 DOI: 10.1126/science.1153825

Bradley E, & Stuart J (1998). Using chaos to generate variations on movement sequences. Chaos (Woodbury, N.Y.), 8 (4), 800-807 PMID: 12779786

Spencer, K., Wimpenny, J., Buchanan, K., Lovell, P., Goldsmith, A., & Catchpole, C. (2005). Developmental stress affects the attractiveness of male song and female choice in the zebra finch (Taeniopygia guttata) Behavioral Ecology and Sociobiology, 58 (4), 423-428 DOI: 10.1007/s00265-005-0927-5

Soma, M., Hiraiwa-Hasegawa, M., & Okanoya, K. (2009). Song-learning strategies in the Bengalese finch: do chicks choose tutors based on song complexity? Animal Behaviour, 78 (5), 1107-1113 DOI: 10.1016/j.anbehav.2009.08.002

Kiebel SJ, Daunizeau J, & Friston KJ (2008). A hierarchy of time-scales and the brain. PLoS computational biology, 4 (11) PMID: 19008936

Hosino, T., & Okanoya, K. (2000). Lesion of a higher-order song nucleus disrupts phrase level complexity in Bengalese finches NeuroReport, 11 (10), 2091-2095 DOI: 10.1097/00001756-200007140-00007

Verhoef, Tessa & de Boer, Bart (2011) Cultural emergence of phonemic combinatorial structure in an artificial whistled language, in Proceedings of the 17th International Congress of Phonetic Sciences (ICPhS XVII), Hong Kong, China.