Does your social network determine your rational rationality? When trying to co-ordinate with a number of other people on a cultural feature, the locally rational thing to do is to go with the majority. However, in certain situations it might make sense to choose the minority feature. This means that learning multiple features might be rational in some situations, even if there is a pressure against redundancy. I’m interested in whether there are situations in which it is rational to be bilingual and whether bilingualism is stable over long periods of time. Previous models suggest that bilingualism is not stable (e.g. Castello et al. 2007), therefore an irrational strategy (at least not a primary strategy), but these were based on locally rational learners.
This week we had a lecture from Simon DeDeo on system-wide timescales in the behaviour of macaques. He talked about Spin Glasses and rationality, which got me thinking. A Spin Glass is a kind of magnetised material where the ‘spin’ or magnetism (plus or minus) of the molecules does not reach a consensus, but flips about chaotically. This happens when the structure of the material creates ‘frustrated’ triangles where a molecule is trying to co-ordinate with other molecules with opposing spins, making it difficult to resolve the tensions. Long chains of interconnected frustrated triangles can cause system-wide flips on the order of hours or days and are difficult to study both in models (Ising model) and in the real world.
Ising models have been studied extensively, and have been applied to language (e.g. Itoh & Ueda, 2004, Stauffer et al. 2007) and, indeed, been applied to bilingualism (Castello et al. 2007). The model imagines each molecule to be a person, and their spin to be their choice of langauge or linguistic variant (typically 2 languages for simplicity and tractability). Speakers interact with a sub-set of all speakers in a social network, just like molecules joined by molecular bonds. At each time step, speakers consider the languages spoken by the people they are connected to and choose whether to stick with their current langauge or change. The models can be used to explore when a system will reach consensus – where everybody will speak the same langauge. A rational approach to this problem as an individual is to switch to the langauge spoken by the majority of the people you are connected to. This is the assumption made by most models.
However, if the social network is complex, then it may be more rational to consider the system-level situation in order to avoid a Spin Glass dynamic (although we’re assuming some kind of group-level goal, here). Since speakers in this model have no information outside their immediate connections, one possibility is to just choose a language at random with a certain probability. Let’s call this a speaker’s ‘rationality’ (or local rationality): With a rationality of 1.0, a speaker always changes to the majority langauge. With a rationality of 0.5, the speaker changes to the majority langauge half the time and randomly chooses a langauge the other half. Adding a bit of noise into the model can help resolve frustrated loops and reach consensus.
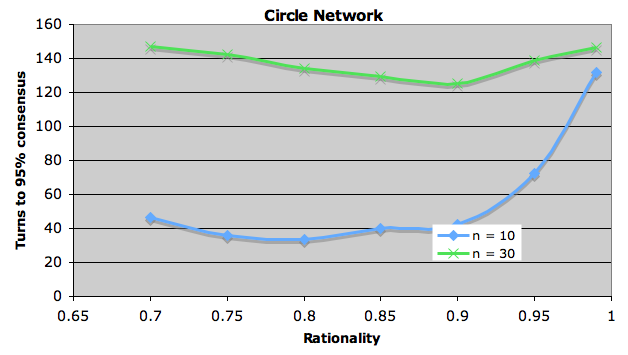
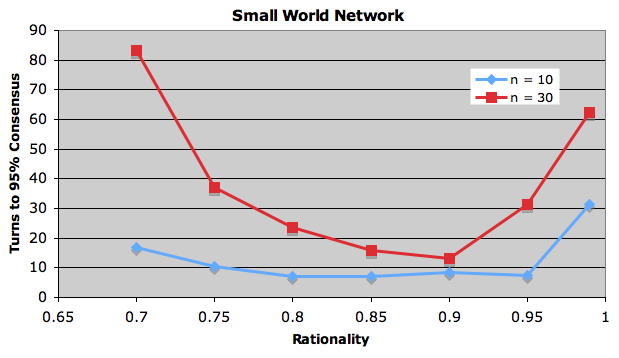
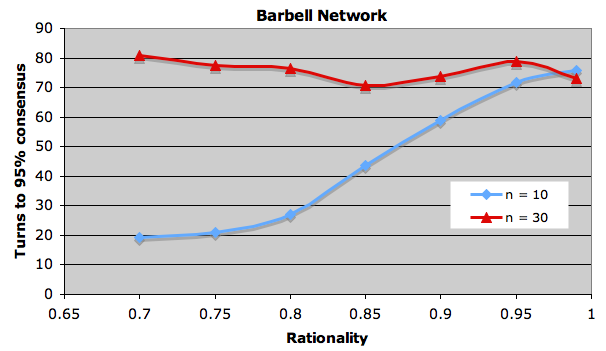
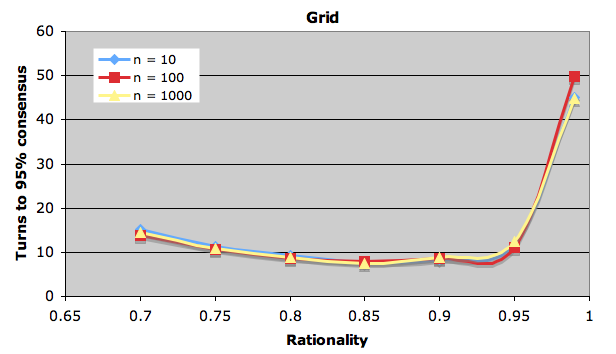
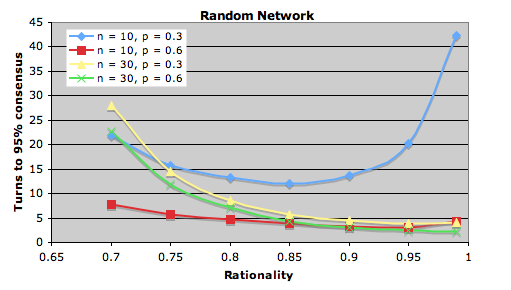
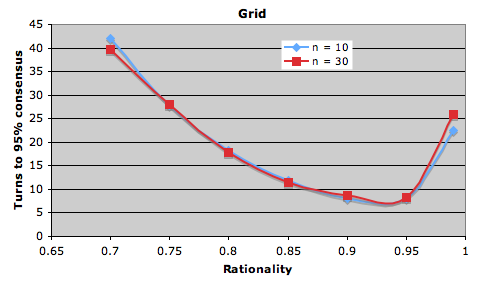
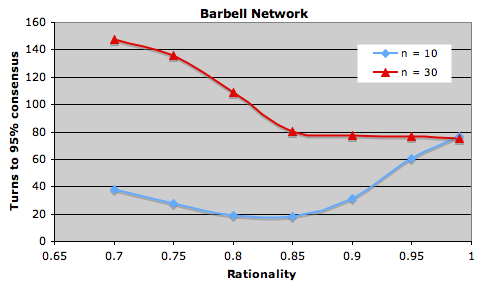
My question is – does the optimal rationality depend on the social network? I built a model and ran some experiments. Let’s assume a number of speakers n in a social network of type k who start with random language settings (2 possible langauges). At each timestep every speaker changes its langauge to the majority spoken by those speakers connected to it (absolute majority, all speakers change simultaneously) with a probability r (the rationality), or choose a language at random otherwise. Below are some results showing the average number of time steps to reach 95% consensus for different kinds of network and different levels of rationality (average over 1000 runs, lower scores = more rational setting).
The striking thing is the variation in optimal rationality profiles. Both the type of network and the number of speakers has an effect.
Here’s a random network with two density settings (probabilities of 0.3 an 0.6 of a possible connection being made).
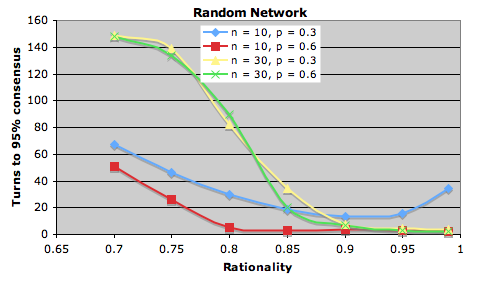
We can also specify that the learner chooses the minority language with a certain probability (irrational), instead of choosing a language randomly (in the current model with only two languages, this is less damaging than a model with many more languages). We see some differences when doing this:
It seems that the rational approach to cultural co-ordination may be to be not entirely rational, depending on the kind of social network you live in. However, learners may not have access to this information, although some cases might be obvious such as knowing that there are two separate communities. It might be obvious, but if you live in a society where there are two communities that interact more within than between themselves, then it might be a good idea to keep your options open rather than going with the majority.
Open questions:
- How does this relate to the large literature on Ising Models? Someone has probably done this kind of thing before.
- The model doesn’t currently allow bilingualism, this could be added (see Castello et al., 2007).
- How is the optimal rationality related to more appropriate network statistics, e.g. transitivity, average degree etc?
- Can an individual learn the optimal rationality? For example, by updating their rationality according to their ‘success’ the last timestep? Or by considering the regularities of the system-wide switches? If so, what is the evolutionary stable distribution?
- Is this ‘rationality’ too far beyond the cognitive capabilities of the individual?
- The results above are only based on relatively small sample sizes (1000 runs for each point), a better monte carlo approach is needed, which will either require re-programming in a faster langauge, e.g. C or a mathematical approach with eigenvectors etc.
Example code here.
ITOH, Y., & UEDA, S. (2004). The Ising model for changes in word ordering rules in natural languages Physica D: Nonlinear Phenomena, 198 (3-4), 333-339 DOI: 10.1016/j.physd.2004.09.006
STAUFFER, D., CASTELLO, X., EGUILUZ, V., & SANMIGUEL, M. (2007). Microscopic Abrams–Strogatz model of language competition Physica A: Statistical Mechanics and its Applications, 374 (2), 835-842 DOI: 10.1016/j.physa.2006.07.036
Castelló, X., Loureiro, L., Eguíluz , V. M., & San Miguel, M. (2007). The fate of bilingualism in a model of language competition Advancing Social Simulation: The First World Congress, 83-94