A random walk model of linguistic complexity

EDIT: Since writing this post, I have discovered a major flaw with the conclusion which is described here.

One of the problems with large-scale statistical analyses of linguistic typologies is the temporal resolution of the data.  Because we only typically have single measurements for populations, we can’t see the dynamics of the system.  A correlation between two variables that exists now may be an accident of more complex dynamics.  For instance, Lupyan & Dale (2010) find a statistically significant correlation between a linguistic population’s size and its morphological complexity.  One hypothesis is that the language of larger populations are adapting to adult learners as they comes into contact with other languages.  Hay & Bauer (2007) also link demography with phonemic diversity.  However, it’s not clear how robust these relationships are over time, because of a lack of data on these variables in the past.

To test this, a benchmark is needed.  One method is to use careful statistical controls, such as controlling for the area that the language is spoken in, the density of the population etc.  However, these data also tend to be synchronic.  Another method is to compare the results against the predictions of a simple model.  Here, I propose a simple model based on a dynamic where cultural variants in small populations change more rapidly than those in large populations.  This models the stochastic nature of small samples (see the introduction of Atkinson, 2011 for a brief review of this idea).  This model tests whether chaotic dynamics lead to periods of apparent correlation between variables.  Source code for this model is available at the bottom.

Model

A linguistic group has a population p and a linguistic complexity c.  The linguistic complexity could represent morphological complexity or phonological inventory etc.  Both variables evolve according to a random walk.  That is, at each time step, the population will randomly increase or decrease a small amount (given upper and lower bounds).  The change in complexity, however, is bounded by the population size.  In a small population, the complexity can change rapidly, while in a large population, it only changes slowly.  The absolute change in complexity is in relation to the inverse of the log population size.

The group populations are sampled from the (log) linguistic populations in the Ethnologue.  The complexity measure c is initialised randomly for each group.  The model was run for 1000 timesteps.  The main measure was the proportion of timesteps where there was a significant negative correlation (Pearson’s r) between population size and complexity (Lupyan & Dale find a negative correlation).

Results

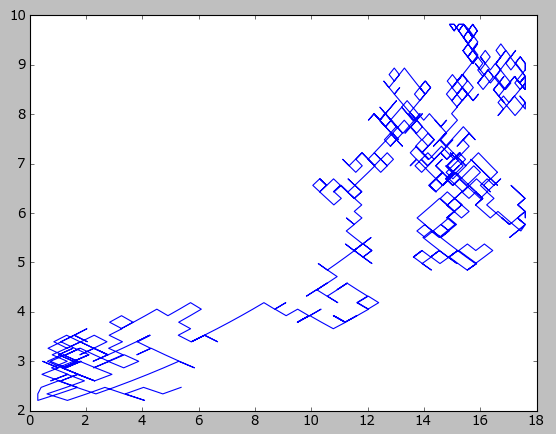
Here’s a graph showing how the variables for a single group changes over time (complexity on the x axis, log populaiton size on the y axis).  The trajectory looks like Brownian motion:

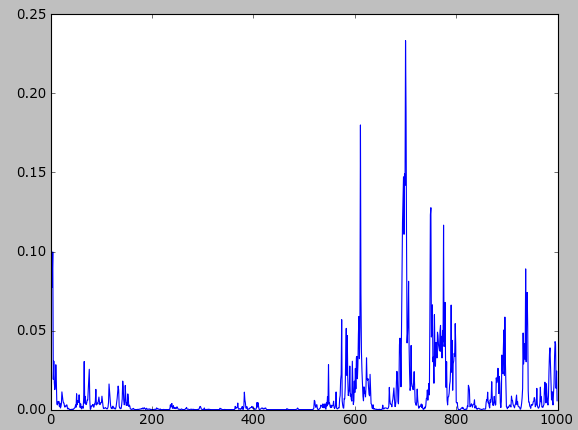
For the full sample of groups from the Ethnologue, the correlation between population size and complexity was significant at the 0.01 level 39.7% of the time on average (over 10 runs).  This is perhaps surprisingly high.  All of these were for negative correlations.  Below is a graph showing the probability of the correlation for a single run (p value on the y axis, time along the bottom).  The p value decreases rapidly (it starts around 0.1), but fluctuates considerably as well:

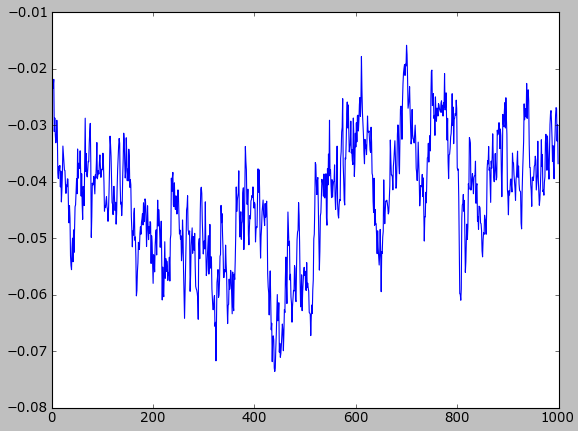
Here’s the correlation coefficient for the same run.  Note that the correlation is very small (between -0.03 and -0.06):

However, this seems to be affected by the number of groups in the model.  With only 500 groups, the number of timesteps where the correlation is significant at the 0.01 level is only 3% (average of 50 runs, 9.6% at the 0.05 level).  That is, the correlation appears chaotically, but a larger sample helps dampen the stochastic nature of the model.

Conclusion

Linguistic complexity in this model changes more rapidly for smaller groups. Population size only affected the rate of change of complexity- not the direction of change.  Even so, for a non-trivial proportion of the time there was a significant correlation between population size and complexity.  This may be caused by unstable dynamics which produce periods of significant correlation along with the effects of upper and lower bounds.

Analyses of synchronic data (such as linguistic typologies) assume that the correlations are constant over time.  However, the correlations could arise from the variables oscillating on a simple dynamic trajectory.  Interpreting the model above very liberally, some recent studies may have caught the system in one of these states.  This model could be used to estimate the probability of this happening, and so be used as an additional benchmark.

There are many problems with this model.  First, the amount of variation explained by the model is extremely low, and probably negligible in studies controlling for many other sources of variance.  Also, all populations grow at the same rate.  The rates at which linguistic complexity changes is also probably too high.  More fundamentally, the original assumption that the rate of language change is (linearly) related to population size could be questioned.

Source code

The script used to carry out this analysis is available here, you’ll also need this file for sampling from the populations of the Ethnologue.  It’s a python script requiring numpy and scipy for the model and matplotlib for the plotting.

—-

EDIT:

I forgot to do the really obvious thing and look at the statistics for a fully random walk model (where the step size for complexity is not related to population size).  This model produced a significant negative correlation at the 0.01 level only 1.1% of the time (over 10 runs, 2.9% at the 0.05 level).   Positive correlations also appeared more often than the connected model.  It seems like the connection between rate of change and population size has a significant effect on the number of negative correlations.

EDIT: Since writing this post, I have discovered a major flaw with the conclusion which is described here.

—-

Lupyan G, & Dale R (2010). Language structure is partly determined by social structure. PloS one, 5 (1) PMID: 20098492

Hay, J., & Bauer, L. (2007). Phoneme inventory size and population size Language, 83 (2), 388-400 DOI: 10.1353/lan.2007.0071

Atkinson QD (2011). Phonemic diversity supports a serial founder effect model of language expansion from Africa. Science (New York, N.Y.), 332 (6027), 346-9 PMID: 21493858